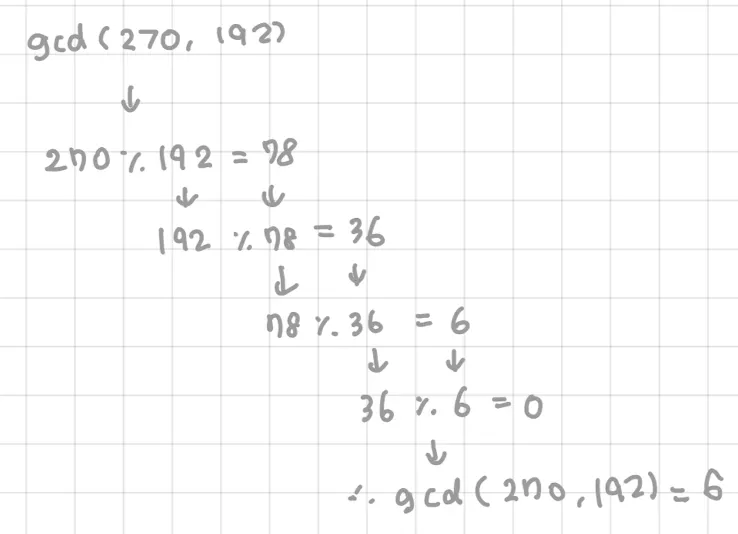정의
•
두 수의 최대 공약수를 구하는 알고리즘
과정
1.
큰 수에서 작은 수로 나누는 mod 연산을 수행
2.
각 단계에서 작은 수와 mod 연산 결과값으로 mod 연산을 수행
3.
2번을 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택
특징 및 팁
•
시간복잡도: O(log(max(a,b)))
•
재귀 형태로 쉽게 구현 가능
•
배수 관계인 두 수의 최대 공약수를 구하면, 둘 중 작은 수가 최대 공약수임
◦
유클리드 호제법에서 나머지가 0이 되는 순간 작은 수를 최대 공약수로 선택하는 이유임
•
기존의 최대 공약수 구하는 방법은 두 수의 공통된 약수를 알아야 하는데, 두 수가 너무 커서 공통된 약수를 알기 어려운 경우에 두 수를 작게 만들기 위해 유클리드 호제법 사용하는 거임
◦
gcd(270, 192) == gcd (192, 78) == gcd (78, 36) == gcd (36, 6) 이기 때문임
◦
gcd(270, 192) 대신 gcd(36, 6)의 값을 구하는 편이 쉬움
◦
36과 6은 배수 관계라서 둘 중 작은 값인 6을 최대 공약수로 바로 택하면 되기 때문임
•
최소 공배수는 유클리드 호제법을 이용해 구한 최대 공약수를 이용해 구하면 쉬움
◦
A * B = GCD(A, B) * LCM(A, B)
예시
코드
int gcd (int a, int b) {
if (b == 0) return a;
return gcd(b, a%b);
}
int gcdWithLoop (int a, int b) {
while (b != 0) {
int r = a % b;
int a = b;
int b = r;
}
return a;
}
int lcm (int a, int b) {
return a / gcd(a,b) * b; // int overflow 방지하기 위해 곱셈보다 나눗셈 먼저 진행
}
Java
복사
증명
gcd(270, 192) == gcd (192, 78) == gcd (78, 36) == gcd (36, 6) 가 가능한 이유
참고