정의
•
여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union 연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 (자신의 대표 노드를 찾아주는) find 연산으로 구성되어 있는 알고리즘
특징
•
union 할 땐 항상 대표 노드끼리 연결함
•
연결된 걸 표현할 땐 배열에서 자식 노드를 인덱스로 한 값에 대표 노드를 저장
•
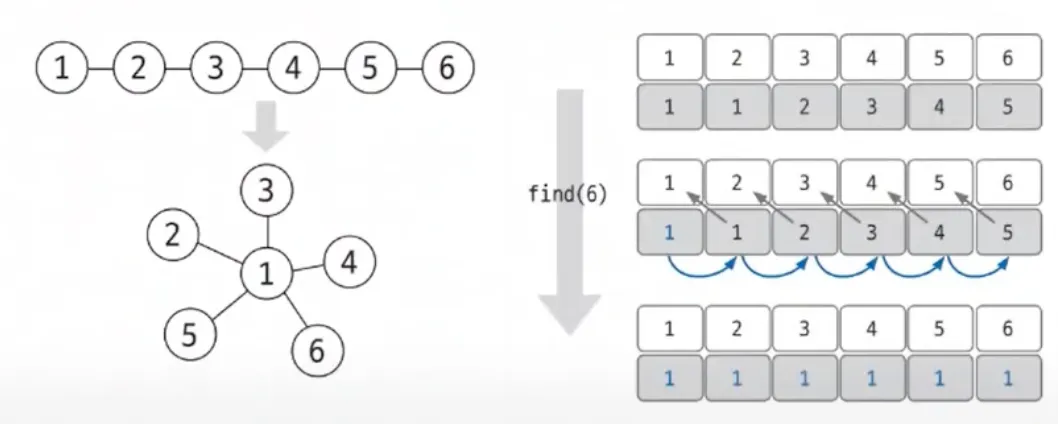
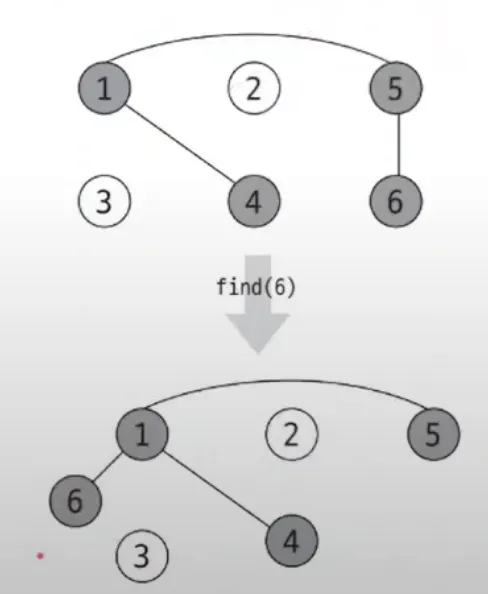
find는 단순히 대표 노드만 찾는 역할만 하는 것이 아니라 그래프를 정돈하고 시간 복잡도를 향상시킴
◦
경로 압축의 효과 : 여러 노드에서 거쳐야 하는 경로에서 그래프 변형해 더 짧은 경로로 갈 수 있도록 해 시간 복잡도 효과적으로 줄임
◦
예시) find 연산 속도가 O(1)로 변경됨
과정
1.
대표 노드를 저장하는 배열에 인덱스를 그대로 값으로 넣어주어 초기화
2.
2개의 노드 선택해 각각의 대표 노드를 찾아(find해) union 연산 수행
•
find
1.
대상 노드 배열에 index 값과 value 값이 동일한지 확인
2.
동일하지 않으면 value 값이 가리키는 index 위치로 이동
3.
이동 위치의 index 값과 value 값이 같을 때까지 1~2번을 반복 (재귀 함수로 구현)
4.
대표 노드에 도달하면 재귀 함수를 빠져나오면서, 거치는 모든 노드 값을 루트 노드값(=대표 노드 값)으로 변경
예시
작은 값을 대표 노드로 둘 때
•
초기화 → [1,2,3,4,5,6]
•
union(1, 4) → find(1)=1, find(4)=4 → [1,2,3,1,5,6]
•
union(5,6) → find(5)=5, find(6)=6 → [1,2,3,1,5,5]
•
union(4,6) → find(4)=1_find(1)=1, find(6)=5_find(5)=5 → union(1,5) → [1,2,3,1,1,5]
•
union(2,6) → find(2)=2, find(6)=5_find(5)=1_find(1)=1 → [1,2,3,1,1,1] → union(2,1) → [1,1,3,1,1,5]
◦
[1,2,3,1,1,1] → find(6)=5 에 대해 후엔 find(6)=1이 나오게 변경
코드
private static int[] graph;
private static void solution(int n) {
initGraph(n);
union(1, 2);
}
private static void initGraph(int n) {
graph = new int[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = i;
}
}
private static int find(int target) {
if (graph[target] == target)
return target;
int parent = find(graph[target]);
graph[target] = parent;
return parent;
}
private static void union(int a, int b) {
int aParent = find(a);
int bParent = find(b);
if (aParent <= bParent) {
graph[bParent] = aParent;
} else {
graph[aParent] = bParent;
}
}
Java
복사
참고