트리
정의
•
무방향이면서 사이클이 없는 연결 그래프
◦
노드와 에지로 연결된 그래프의 특수한 형태
특징
•
임의의 에지를 추가하면 사이클이 생김
•
임의의 두 에지를 제거하면 연결 그래프가 아니게 됨
•
임의의 노드를 루트 노드로 만들 수 있음
◦
트리가 마치 구슬과 실로 연결되어 있는 모양이라고 생각할 때, 아무 구슬 하나를 잡고 위로 올린 상황
•
루트가 정해진 상태에선 부모를 가지지 않는 1개의 루트 노드가 존재하고, 루트 노드를 제외한 노드들은 단 1개의 부모 노드를 가짐
◦
임의의 두 노드를 이어주는 경로가 유일함. 이때 경로는 정점이 중복해서 나오지 않는 경로를 의미함
•
V개의 노드를 가지고 V-1개의 에지를 가짐
◦
노드가 1개이고 에지가 없는 그래프도 트리임
•
트리의 부분 트리 역시 트리의 모든 특징을 따름
용어
•
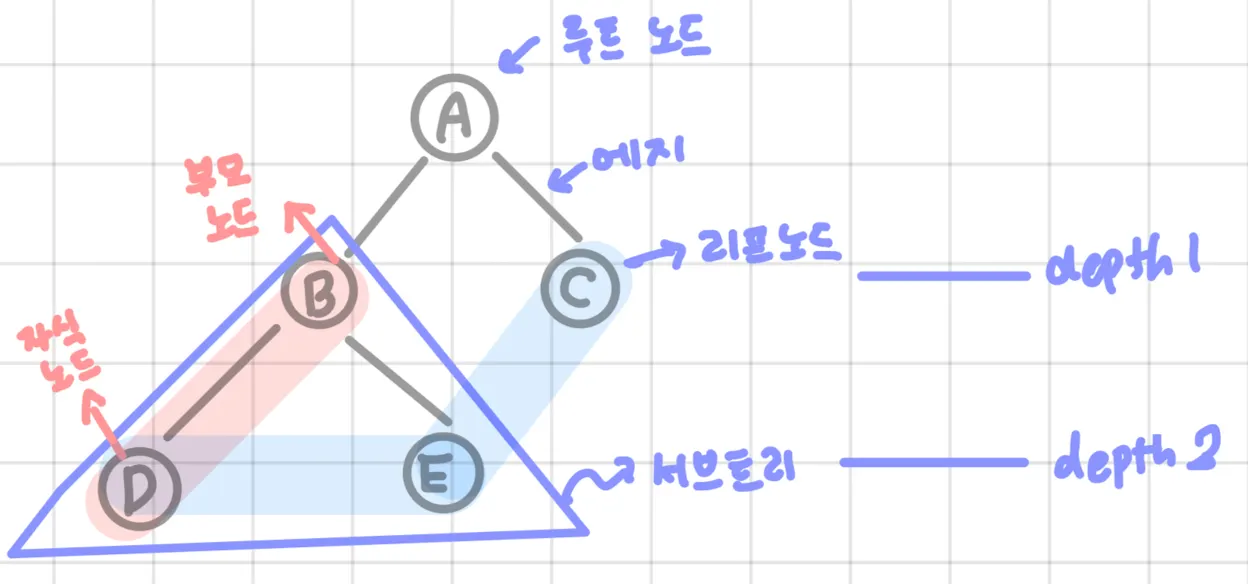
에지: 노드와 노드의 연결 관계 나타내는 선
•
노드: 데이터의 index와 value를 표현하느 요소
◦
루트 노드: 트리에서 가장 상위에 존재하는 노드
◦
부모 노드: 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
◦
자식 노드: 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
◦
리프 노드: 트리에서 가장 하위에 존재하는 노드 (자식 노드가 없는 노드)
•
서브 트리: 전체 트리에 속한 작은 트리 (부분 트리)
•
노드의 차수: 연결된 자식의 수→ A의 차수: 2
•
노드의 크기: 자신을 포함한 자손의 수 (자식 x) → A의 크기: 5
•
노드의 깊이: 루트와의 거리 → B의 깊이: 1
•
트리의 차수: 트리의 최대 차수 → 차수: 2
•
트리의 깊이: 가장 깊숙이 있는 노드의 깊이. 높이라고도 부름 → 높이: 2
팁
•
코딩테스트에서 등장하는 트리 문제 유형
1.
그래프로 푸는 트리
•
dfs, bfs : 트리를 인접리스트로 표현해서 품
2.
트리만을 위한 문제
•
이진트리, 세그먼트 트리(인덱스 트리), LCA(최소공통조상) : 트리를 1차원 배열로 표현해서 품
◦
부모 노드로 이동 : index / 2
◦
자식 노드로 이동 : index * 2 ( + 1)
과정 (BFS/DFS)
•
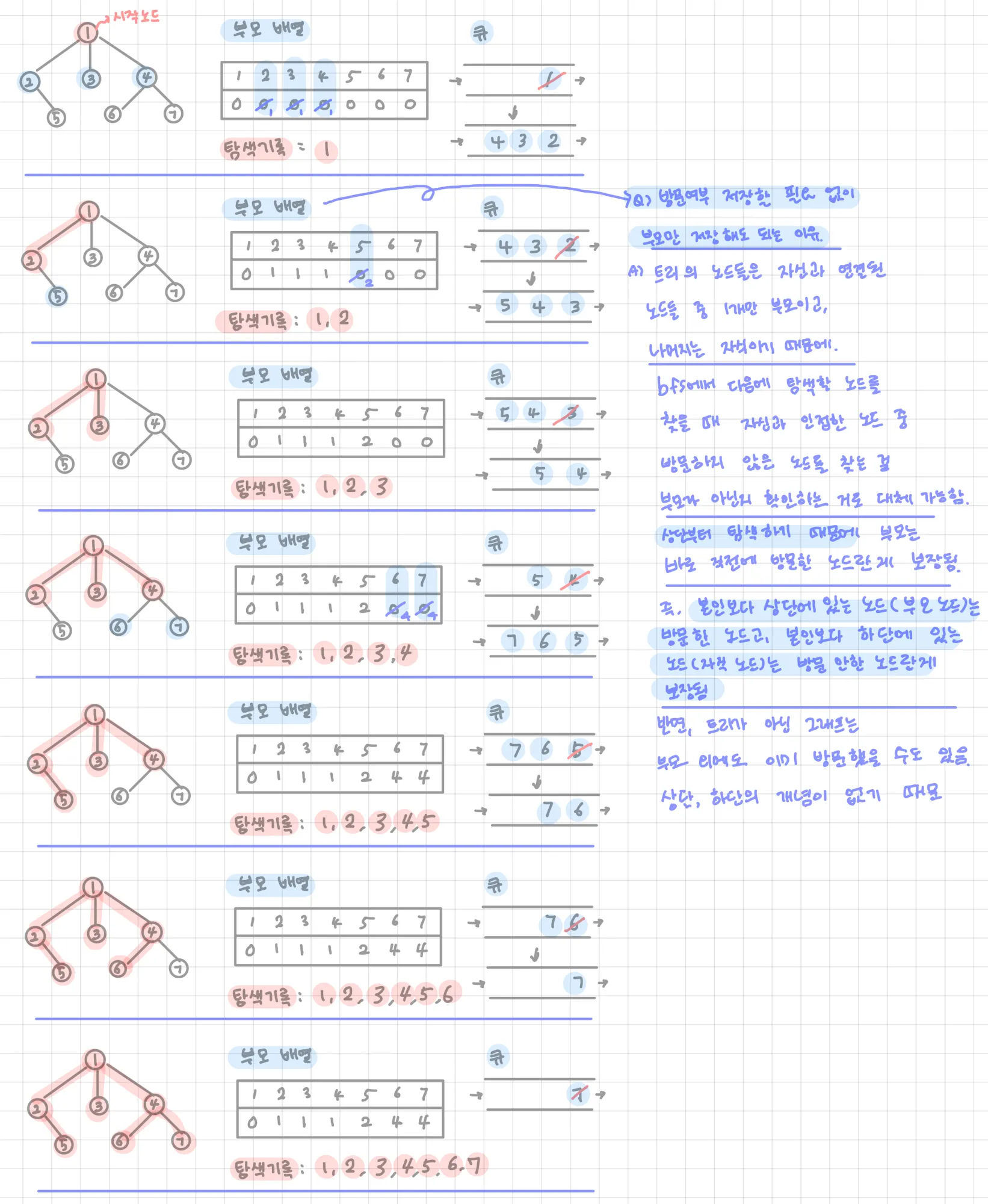
특징) 트리의 어떤 노드와 연결된 노드들은 1개만 부모이고 나머진 전부 자식이란 성질 이용해서 visited 배열 대신 부모 배열 이용해 처리 가능
•
BFS
1.
초기화하기
•
트리(그래프)를 인접리스트로 표현하기
•
부모 배열(부모 정보 저장) 만들기 (전부 0으로 초기화 → 루트의 부모도 0)
•
임의의 잡은 시작점을 루트로 정해서 큐에 넣기
2.
큐에서 빼온 노드(현재 노드)에 대해 출력하기
3.
현재 노드의 인접 노드들 중 부모 노드를 제외한 나머지 노드들을 큐에 넣고, 해당 노드들의 부모 정보를 현재 노드로 저장하기
4.
큐가 빌 때까지 단계 2부터 다시 반복
•
DFS (BFS에서 큐만 스택으로 바뀜)
1.
초기화하기
•
트리(그래프)를 인접리스트로 표현하기
•
부모 배열(부모 정보 저장) 만들기 (전부 0으로 초기화 → 루트의 부모도 0)
•
임의로 잡은 시작점을 루트로 정해서 스택에 넣기
2.
스택에서 빼온 노드(현재 노드)에 대해 출력하기
3.
현재 노드의 인접 노드들 중 부모 노드를 제외한 나머지 노드들을 스택에 넣고, 해당 노드들의 부모 정보를 현재 노드로 갱신하기
4.
스택이 빌 때까지 단계 4부터 다시 반복
예시 (BFS)
코드 (BFS/DFS) (with 백준 11725)
private static LinkedList<Integer>[] tree;
private static int[] parent;
private static int[] solution(int n, int[][] numbers) { // 노드 수는 n, 에지 수는 n-1
// 1. 트리를 인접 리스트로 표현하고, 부모배열 생성(0으로 초기화)하기
tree = new LinkedList[n + 1];
for (int i = 1; i <= n; i++) {
tree[i] = new LinkedList<>();
}
for (int i = 1; i < n; i++) {
int start = numbers[i][0];
int end = numbers[i][1];
tree[start].add(end);
tree[end].add(start);
}
parent = new int[n + 1]; // 0은 비우고, 노드 개수만큼 생성
// 2. bfs 혹은 dfs (시작점은 1)
// bfs(1);
// dfs(1);
dfsWithRecursion(1);
return parent;
}
private static void bfs(int start) {
// 1. 큐에 시작점(루트) 넣기
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
// 2. bfs (큐가 빌 때까지 반복)
while (!queue.isEmpty()) {
// 2-1. 큐에서 뺀 노드(현재 노드)를 출력하기
int current = queue.remove();
System.out.println(current);
// 2-2. 현재 노드의 인접 노드들 중 부모 노드 제외하고 나머지를 큐에 넣고, 해당 노드들의 부모로 현재 노드를 저장하기
for (int next : tree[current]) {
if (next == parent[current]) { // current의 인접 노드 중 current의 부모 노드는 제외
continue;
}
parent[next] = current; // current의 자식 노드의 부모로 current를 저장
queue.add(next);
}
}
}
private static void dfs(int start) {
// 1. 스택에 시작점(루트) 넣기
Stack<Integer> stack = new Stack<>();
stack.push(start);
// 2. dfs (스택이 빌 때까지 반복)
while (!stack.isEmpty()) {
// 2-1.스택에서 뺀 노드(현재 노드)를 출력하기
int current = stack.pop();
System.out.println(current);
// 2-2. 현재 노드의 인접 노드들 중 부모 노드 제외하고 나머지를 스택에 넣고, 해당 노드들의 부모로 현재 노드를 저장하기
for (int next : tree[current]) {
if (next == parent[current]) { // current의 인접 노드 중 current의 부모 노드는 제외
continue;
}
parent[next] = current; // current의 자식 노드의 부모로 current를 저장
stack.push(next);
}
}
}
private static void dfsWithRecursion(int current) {
// 2-1.현재 노드를 출력하기
System.out.println(current);
// 2-2. 현재 노드의 인접 노드들 중 부모 노드 제외하고 나머지 노드들의 부모로 현재 노드를 저장하고, 해당 노드들 탐색하기
for (int next : tree[current]) {
if (next == parent[current]) {
continue;
}
parent[next] = current;
dfsWithRecursion(next); // 2. dfs (모든 노드의 자식 노드 다 탐색할 때까지 반복)
}
}
Java
복사
•
현재 노드의 인접 노드들 중 부모 노드 제외한 나머지 노드들 == 현재 노드의 자식 노드들
트라이
정의
•
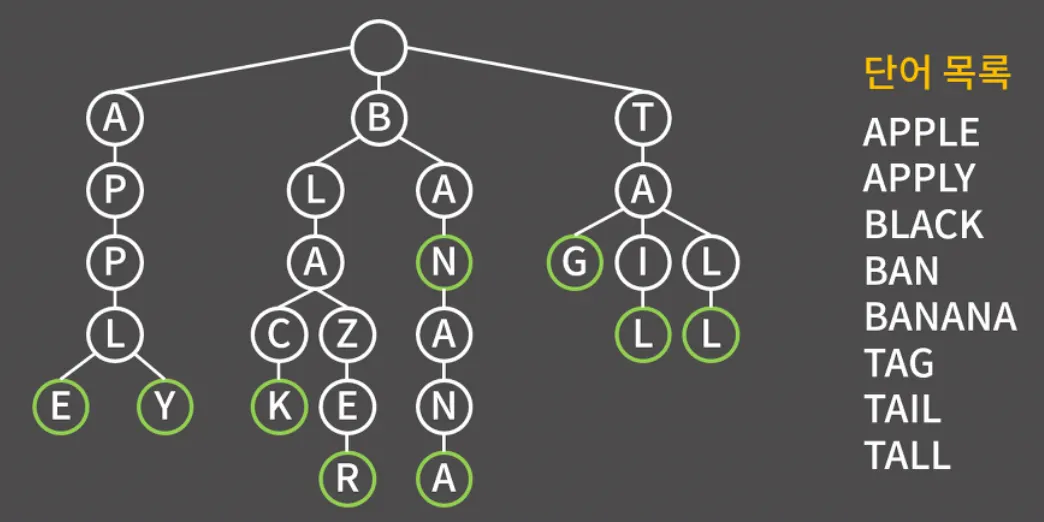
문자열을 효율적으로 처리하기 위한 트리 자료구조
특징
•
시간복잡도: 단어 S를 삽입/탐색/삭제 시 O(|S|)
•
공간복잡도: 문자열을 그냥 배열에 저장하는 것보다 최대 (4*글자의 종류)배 만큼 더 사용
◦
트라이 삭제하더라도 이전에 삽입한 정점들은 계속 메모리에 남아있게 되어 메모리 측면에서 비효율적이고 삭제가 계속 발생하는 환경에선 트라이 적합하지 않음
과정
•
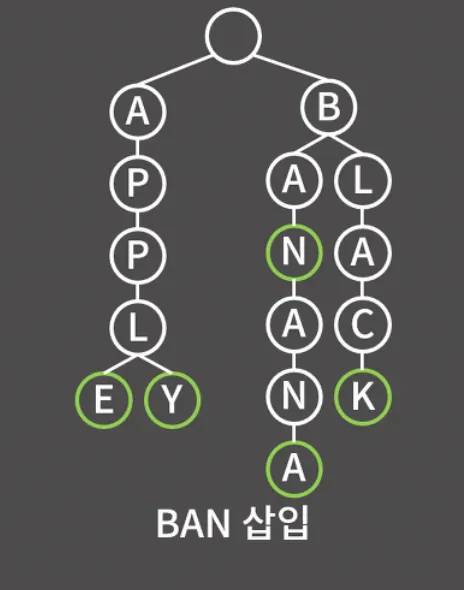
삽입(Insert)
◦
루트부터 바라보고 원하는 단어의 첫 알파벳부터 순서대로 삽입함
◦
현재 바라보는 노드의 자식에 알파벳이 없으면 해당 노드의 자식으로 추가 후, 새로 추가한 노드를 바라봄
◦
원하는 단어의 모든 알파벳 다 넣으면 마지막 글자엔 별도의 표시 해둠
•
검색(Fetch)
◦
루트부터 바라보고 원하는 단어의 첫 알파벳부터 검색함
◦
원하는 단어의 마지막 알파벳까지 다 찾으면 마지막 노드에 마지막 문자라는 표시가 있는지 확인함
•
제거(Erase)
◦
루트부터 바라보고 원하는 단어의 첫 알파벳부터 검색함
◦
원하는 단어의 마지막 단어까지 다 찾으면 마지막 노드에 있는 마지막 문자라는 표시를 제거함
▪
노드 자체를 제거하지 않음
참고