들어가기 전 용어 정의
•
탐색 : 첫 방문 이후 실제 탐색이 이뤄짐
•
방문 : 첫 방문이 이뤄짐
짧게 요약: 방문 할 수 있는 정점 여러 개 일 때 정점 번호 작은 것 먼저 방문 하고 싶다면.
•
dfs (with 재귀)
◦
인자에 있는 노드에 대해 방문 여부 true로 찍고 동시에 출력하기 (방문과 탐색 동시에)
◦
인접 노드들을 인자에 넣어 재귀 (작은 수부터 함수 호출하기 → 작은 수 먼저 방문)
•
dfs (with 스택)
◦
스택에서 빼온 노드에 대해 출력하기 (탐색은 나중에 함)
◦
인접 노드들의 방문 여부 true로 찍기 (방문을 먼저함)
◦
인접 노드들을 스택에 넣고 반복 (큰 수부터 스택에 넣기 -> 작은 수 먼저 나와 방문)
•
bfs (with 큐)
◦
큐에서 빼온 노드에 대해 출력하기 (탐색은 나중에 함)
◦
인접 노드들의 방문 여부 true로 찍기 (방문을 먼저함)
◦
인접 노드들을 큐에 넣고 반복 (작은 수부터 큐에 넣기 -> 작은 수 먼저 나와 방문)
DFS (깊이 우선 탐색)
•
정의) 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘
•
특징)
◦
그래프 완전 탐색 기법 중 하나
◦
DFS 탐색 방식은 후입 선출(LIFO) 특성을 가짐
▪
주로 재귀 함수나 스택 자료 구조를 이용해 구현함
▪
재귀 사용 시 스택 오버 플로우 유의 필요함
◦
시간복잡도 : O(V + E) → 노드 수 : V, 에지 수 : E
▪
한 번 방문한 정점은 다시 방문하지 않으며, 한 정점에서 다음으로 방문할 노드들을 순회하는 횟수가 그 정점의 차수와 같기 때문
◦
DFS 를 응용해 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬 등의 문제를 해결 가능함
•
과정) 스택 이용
1.
DFS 를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
•
그래프를 인접 리스트로 표현하기
•
스택 자료구조에 시작 노드 더하기
•
노드 방문 여부 체크할 배열 초기화 → 시작 노드는 방문 여부 true로 체크하기 (T, F, F, F…)
2.
스택에서 노드를 꺼내고, 꺼낸 노드의 인접 노드 중 방문 안 한 노드를 스택에 삽입하기
a.
pop 수행해 꺼낸 노드를 탐색 순서에 기입하기
b.
꺼낸 노드의 인접 노드들을 스택에 삽입하기
•
이미 방문한 노드는 방문 배열을 바탕으로 재삽입 하지 않음
c.
스택에 삽입한 노드들의 방문 여부 true로 체크하기
3.
2번을 스택에 값이 없을 때까지 반복하기
•
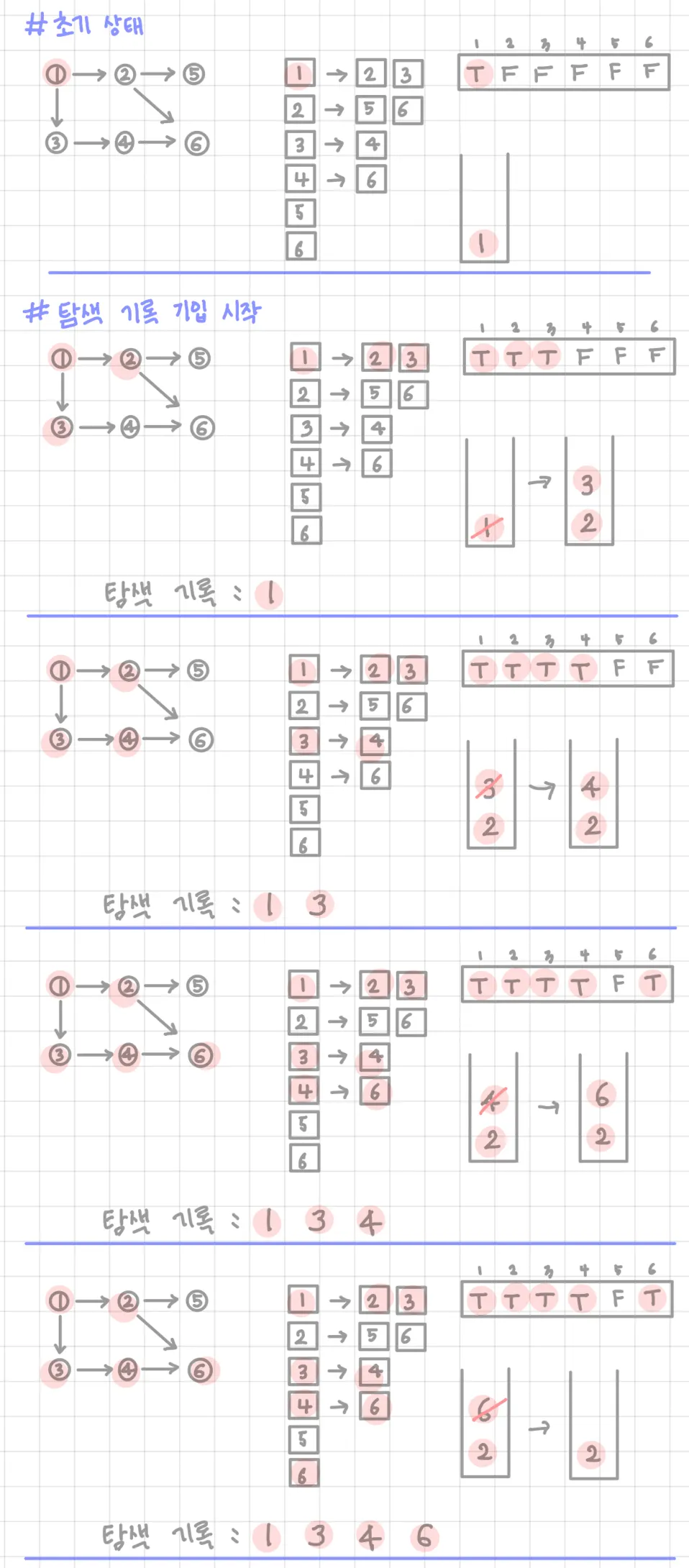
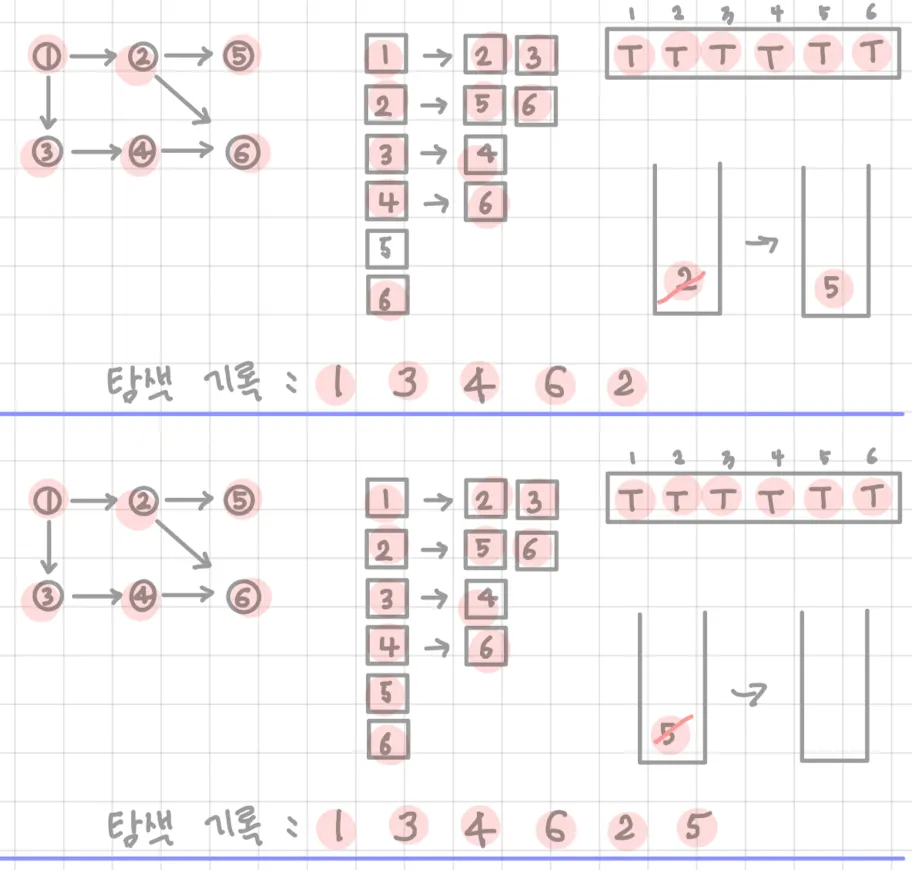
예시) 스택 이용
•
코드) 스택, 재귀 이용
static boolean visited[];
static ArrayList<Integer>[] A;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt(); // 노드 개수
int M = scan.nextInt(); // 에지 개수
int start = scan.nextInt(); // 시작점
// 인접 리스트로 그래프 표현하기
A = new ArrayList[N+1];
for(int i=1; i<=N; i++) { // 노드 초기화
A[i] = new ArrayList<Integer>();
}
for(int i=0; i<M; i++) { // 엣지의 양끝 노드 입력받기
int S = scan.nextInt();
int E = scan.nextInt();
A[S].add(E);
A[E].add(S); // 양방향이라서 양쪽 노드에 엣지 추가
}
for(int i=1; i<=N; i++) { // 번호 작은 것 먼저 방문하기 위해 각 노드의 엣지들 정렬
Collections.sort(A[i]);
}
// 방문 배열 초기화하기
visited = new boolean[N+1];
dfs(start);
visited = new boolean[N+1];
dfsWithStack(start);
}
private static void dfs(int Node) {
System.out.print(Node + " "); // 현재 노드 출력하기 (탐색 기록 남기기)
visited[Node] = true; // 현재 노드 방문 기록하기
// 인접한 미방문 노드로 DFS 실행하기
for(int i: A[Node]) { // 현재 노드의 엣지들
if (!visited[i]) {
dfs(i);
}
}
}
private static void dfsWithStack(int startNode) {
Stack<Integer> stack = new Stack<>();
stack.push(startNode);
visited[startNode] = true;
while (!stack.isEmpty()) {
int node = stack.pop();
System.out.print(node + " ");
for (int i = A[node].size() - 1; i >= 0; i--) { // 큰 수부터 접근
int nearNode = A[node].get(i);
if (!visited[nearNode]) {
stack.push(nearNode);
visited[nearNode] = true;
}
}
}
}
Java
복사
BFS (너비 우선 탐색)
•
정의) 시작 노드에서 출발해 시작 노드를 기준으로 가장 가까운 노드를 방문하면서 탐색하는 알고리즘
•
특징)
◦
그래프 완전 탐색 기법 중 하나
◦
BFS 탐색 방식은 선입 선출(FIFO) 특성을 가짐
▪
주로 큐 자료 구조를 이용해 구현함
◦
시간복잡도 : O(V + E) → 노드 수 : V, 에지 수 : E
◦
목표 노드에 도달하는 경로가 여러 개일 때 최단 경로를 보장함
▪
탐색 시작 노드와 가까운 노드를 우선하여 탐색하기 때문임
◦
단순히 방문에서 끝나는 게 아니라, 시작 노드와의 거리를 전부 계산할 수 있음
▪
현재 보는 칸으로부터 추가되는 인접한 칸은 현재 보는 칸보다 1만큼 더 떨어져 있기 때문임
•
과정)
1.
BFS 를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
•
그래프를 인접 리스트로 표현하기
•
큐 자료구조에 시작 노드 더하기
•
노드 방문 여부 체크할 배열 초기화 → 시작 노드는 방문 여부 true로 체크하기 (T, F, F, F…)
2.
큐에서 노드를 꺼내고, 꺼낸 노드의 인접 노드 중 방문 안 한 노드를 큐에 삽입하기
a.
poll 수행해 꺼낸 노드를 탐색 순서에 기입하기
b.
꺼낸 노드의 인접 노드들을 큐에 삽입하기
•
이미 방문한 노드는 방문 배열을 바탕으로 재삽입 하지 않음
c.
큐에 삽입한 노드들의 방문 여부 true로 체크하기
3.
2번을 큐에 값이 없을 때까지 반복하기
•
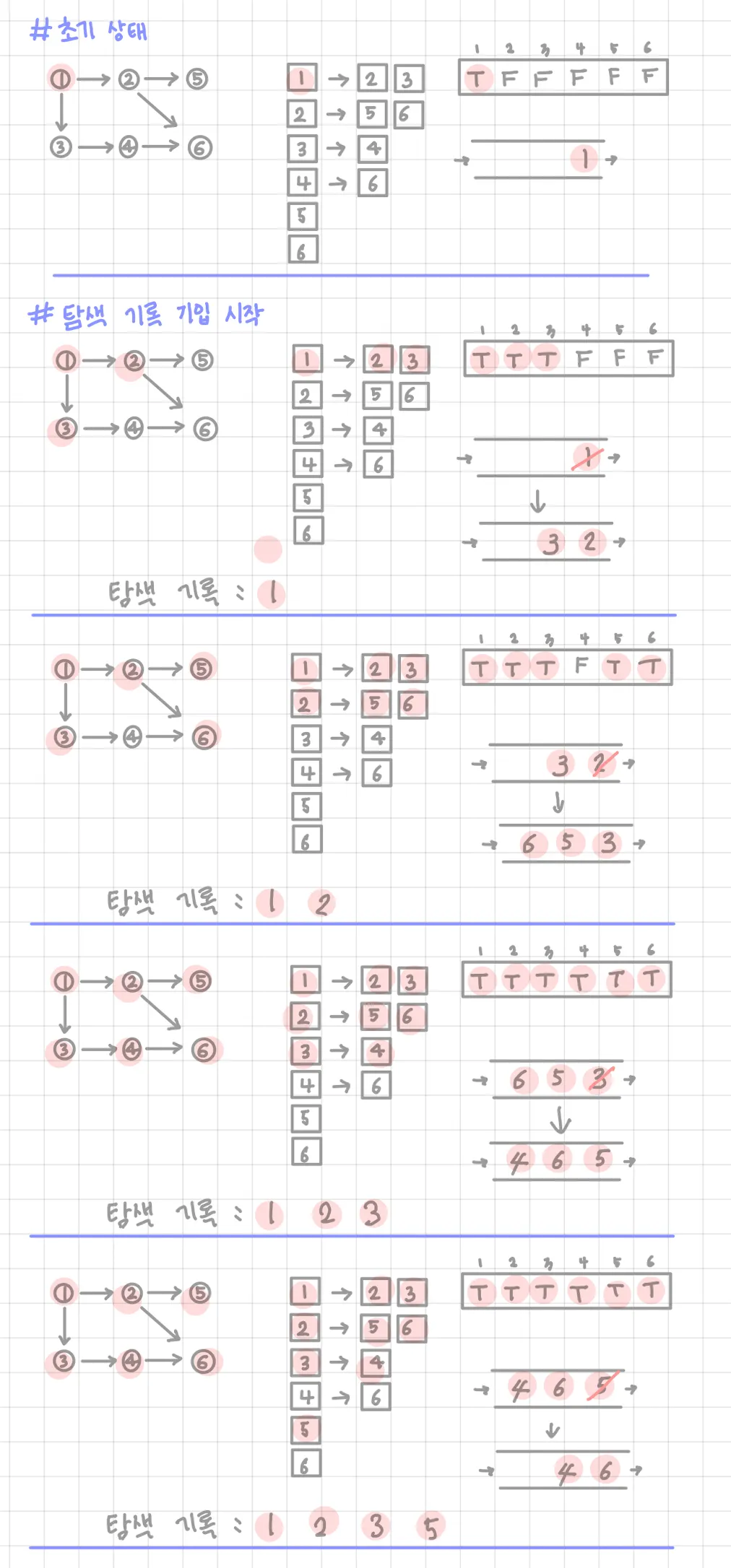
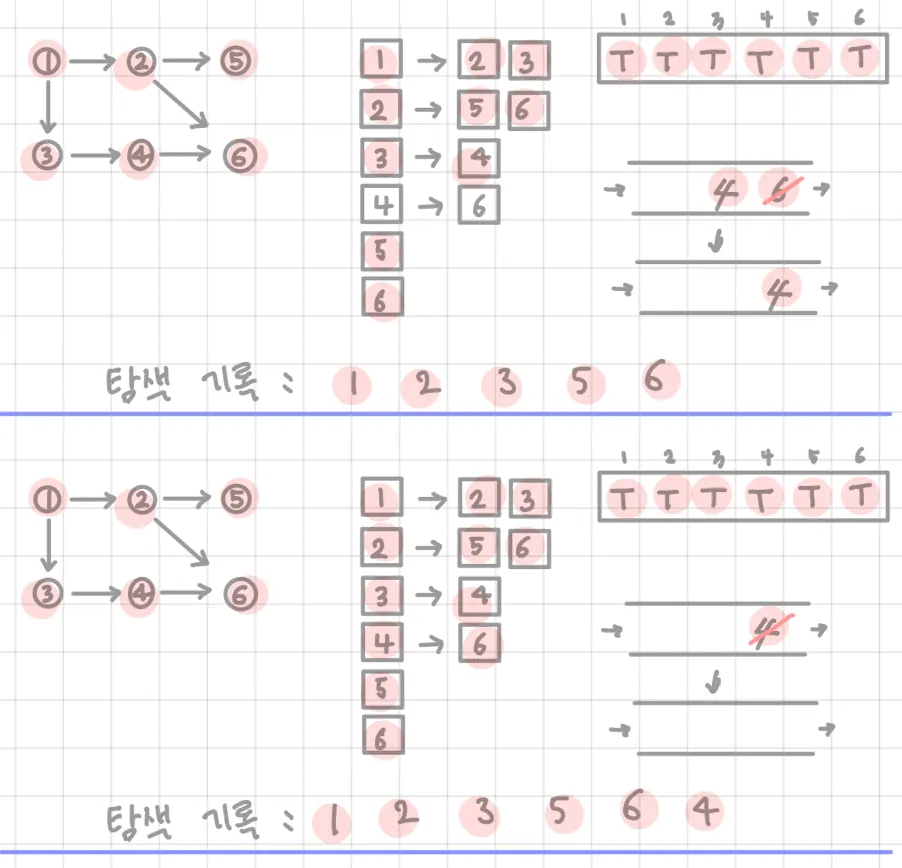
예시)
•
코드)
static boolean visited[];
static ArrayList<Integer>[] A;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt(); // 노드 개수
int M = scan.nextInt(); // 에지 개수
int Start = scan.nextInt(); // 시작점
// 1. 인접 리스트로 그래프 표현하기
A = new ArrayList[N+1];
for(int i=1; i<=N; i++) { // 노드 초기화
A[i] = new ArrayList<Integer>();
}
for(int i=0; i<M; i++) { // 엣지의 양끝 노드 입력받기
int S = scan.nextInt();
int E = scan.nextInt();
A[S].add(E);
A[E].add(S); // 양방향이라서 양쪽 노드에 엣지 추가
}
for(int i=1; i<=N; i++) { // 번호 작은 것 먼저 방문하기 위해 각 노드의 엣지들 정렬
Collections.sort(A[i]);
}
// 방문 배열 초기화하기
visited = new boolean[N+1];
// 시작 노드 큐에 삽입하기
BFS(Start);
}
public static void BFS(int Node) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(Node); // 시작 노드 큐에 삽입하기
visited[Node] = true; // 시작 노드 방문 기록하기
// 인접한 미방문 노드로 BFS 실행하기
while(!queue.isEmpty()) {
// 큐에서 현재 노드 가져와서 출력하기
int new_Node = queue.poll();
System.out.print(new_Node + " "); // 현재 노드 출력하기 (탐색 기록 남기기)
for(int i : A[new_Node]) { // 현재 노드의 엣지들
if(!visited[i]) {
queue.add(i); // 인접한 미방문 노드 큐에 삽입하기
visited[i] = true; // 인접한 미방문 노드 방문 기록하기
}
}
}
}
Java
복사
참고