1. 완전 탐색
1) 정의
•
비유) 파일찾기 → 존재하는 모든 폴더에 들어가서 찾음
•
정의) 모든 경우의 수를 찾아서 답을 찾는 방법
•
특징)
◦
가장 확실한 방법
◦
가장 시간이 오래 걸리는 방법
◦
입력(N) 제한이 작다면 완전탐색 의심해 볼만함
•
예시) 백준 2309 일곱 난쟁이
◦
9명 키 합에서 2명 키 뺐을 때 100이 되는 경우 모두 찾기 → 9C2
2) 종류
[1] 브루트포스
•
정의) 반복문, 조건문을 이용해 모두 테스트하는 방법
◦
단순히 for문과 if문으로 모든 경우들을 만들어 답 구함
•
예시)
◦
난쟁이 문제
◦
1부터 100까지 3의 배수 다 더하기 → for (i=1; i<100; i++) {if(i%3==0) sum+=i;}
[2] 비트마스크
•
정의) 2진수 표현 기법을 이용하는 방법
◦
모든 경우의 수가 1 또는 0으로 구성되는 경우
•
예시) 원소가 5개인 집합의 모든 부분집합 구하기
◦
0 0 0 0 0 / 0 0 0 0 1 / 0 0 1 0 1 … → 5자리 2진수로 표현 가능 (쓸지 안 쓸지)
[3] 재귀
•
정의) 자기 자신을 호출하여 작업을 반복 수행하는 방법
◦
재귀함수 : 자기 자신을 호출하는 함수
•
예시) 백준 17478 재귀함수가 뭔가요? (간략히 작성함)
String start = "\"재귀함수가 뭔가요\"\n";
String cont = "\"잘 들어보게.\"\n";
Strng fin = "\"재귀함수는 자기 자신을 호출하는 함수라네.\"\n";
int N; // 반복 횟수
void recur(int level) {
System.out.print("_"*level + start);
if(level==N) { // 종료 조건
System.out.print(fin);
return;
}
System.out.print(cont);
recur(level+1); // 다음 단계
}
Java
복사
•
예시) 원소가 5개인 집합의 모든 부분집합 구하기
public class Main {
static boolean[] isSelected = new boolean[5];
static int[] arr = {0,1,2,3,4};
public static void main(String[] args) {
recur(0);
}
public static void recur(int level) {
if(level==5) { // 종료 조건
for(int i=0; i<5; i++){
if(isSelected[i]) System.out.print(arr[i] + " ");
}
System.out.println();
return;
}
isSelected[level] = true; // Case 1_ 쓴다 (0,1,2,3,4) (4,
recur(level+1); // 다음 단계 1,2,3,4,5(리턴) 5
isSelected[level] = false; // Case 2_ 안 쓴다 (4) (3,4)
recur(level+1); // 5(리턴) 4,5(리턴)
}
}
Java
복사
출력결과
[4] 순열 nPr
•
정의) n개의 원소 중 r개의 원소를 중복 허용 없이 나열하는 방법
◦
순열에 원소를 하나씩 채워가는 방식
◦
중첩 for문이나 재귀함수로 구현 가능
•
특징) 시간복잡도 O(N!) → N 정말 작을 때만 사용 가능
•
예시) 5C3
public class Main {
public static void main(String[] args) {
int n=5;
int r=3;
int[] arr = {0,1,2,3,4};
int[] perm = new int[n]; // 순열
boolean[] isSelected = new boolean[n]; // 방문 여부
recur(arr, perm, isSelected, 0, n, r);
}
public static void recur(int[] arr, int[] perm, boolean[] isSelected, int level, int n, int r) {
if(level==r) { // 종료 조건
for(int i=0; i<r; i++){
System.out.print(perm[i] + " ");
}
System.out.println();
return;
}
for(int i=0; i<n; i++) {
if(isSelected[i]) continue;
perm[level] = arr[i];
isSelected[i] = true; // Case 1
recur(arr, perm, isSelected, level+1, n, r); // 다음 단계
// perm[level] = 0;
isSelected[i] = false; // Case 2
}
}
}
Java
복사
출력 결과
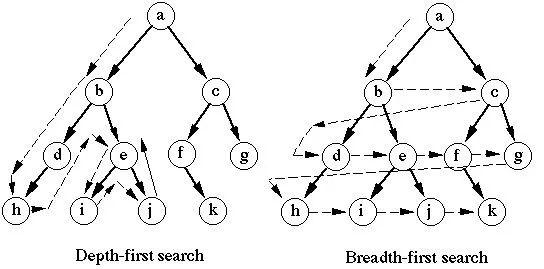
[5] DFS, BFS
•
정의) 그래프에서 모든 정점을 탐색하는 방법
◦
모든 곳을 다 방문한다는 점에서 완전탐색으로 분류 가능
•
종류)
◦
DFS : 깊이 우선 탐색
◦
BFS : 너비 우선 탐색
•
예시) 백준 1260번 DFS와 BFS 프로그램
import java.util.*;
public class Main {
static boolean visited[];
static ArrayList<Integer>[] A;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int N = scan.nextInt(); // 노드 개수
int M = scan.nextInt(); // 에지 개수
int Start = scan.nextInt(); // 시작점
// 1. 인접 리스트로 그래프 표현하기
A = new ArrayList[N+1];
for(int i=1; i<=N; i++) { // 노드 초기화
A[i] = new ArrayList<Integer>();
}
for(int i=0; i<M; i++) { // 엣지의 양끝 노드 입력받기
int S = scan.nextInt();
int E = scan.nextInt();
A[S].add(E);
A[E].add(S); // 양방향이라서 양쪽 노드에 엣지 추가
}
for(int i=1; i<=N; i++) { // 번호 작은 것 먼저 방문하기 위해 각 노드의 엣지들 정렬
Collections.sort(A[i]);
}
// DFS
// 2. 방문 배열 초기화하기
visited = new boolean[N+1];
// 3. 시작 노드 스택에 삽입하기(여기선 스택 대신 재귀함수 사용)
DFS(Start);
System.out.println();
// BFS
// 2. 방문 배열 초기화하기
visited = new boolean[N+1];
// 3. 시작 노드 큐에 삽입하기
BFS(Start);
System.out.println();
}
public static void DFS(int Node) {
System.out.print(Node + " "); // 현재 노드 출력하기
visited[Node] = true; // 현재 노드 방문 기록하기
// 인접한 미방문 노드로 DFS 실행하기
for(int i: A[Node]) { // 현재 노드의 엣지들
if (!visited[i]) {
DFS(i);
}
}
}
public static void BFS(int Node) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(Node); // 시작 노드 큐에 삽입하기
visited[Node] = true; // 시작 노드 방문 기록하기
// 인접한 미방문 노드로 BFS 실행하기
while(!queue.isEmpty()) {
// 큐에서 현재 노드 가져와서 출력하기
int new_Node = queue.poll();
System.out.print(new_Node + " ");
for(int i: A[new_Node]) { // 현재 노드의 엣지들
if(!visited[i]) {
queue.add(i); // 인접한 미방문 노드 큐에 삽입하기
visited[i] = true; // 인접한 미방문 노드 방문 기록하기
}
}
}
}
}
Java
복사
2. 백트래킹
1) 정의
•
비유) 미로찾기 → 길의 끝이 보이면 분기점으로 돌아감
•
정의) 완전 탐색처럼 전부 탐색하지 않고, 가지치기(Pruning)로 가능한 경우의 수를 줄인 것
◦
한정된 조건을 가진 문제를 풀려는 전략
◦
시간이 오래 걸린다는 완전탐색의 단점 보안 (제한 조건 많을수록 시간 단축됨)
•
특징) 주로 재귀함수로 구현
•
예시) 백준 9663 N-Queen
◦
퀸의 특성
▪
상하좌우로 움직일 수 있음
•
같은 행/열에 없어야 함
◦
N*N 체스판에 퀸 N개이므로 각 행/열마다 퀸 한 개씩
▪
대각순으로 움직일 수 있음
•
동일 대각선상에 없어야 함
◦
기울기가 1이거나 -1이면 안됨
◦
경우의 수 구하는 코드
public class Main {
public static int n; // 퀸의 개수
public static int[] arr = new int[100]; // 퀸의 위치 표현한 1차원 배열. 퀸을 하나도 놓지 않은 상태인 0으로 초기화함. 인덱스는 행. 값은 열.
public static int cnt = 0; // 경우의 수
public static int c =0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
nqueen(0);
System.out.print(cnt);
}
// 같은 열이나 같은 대각선에 놓이면 false, 안놓이면 true 반환
public static boolean check(int x) { // x는 현재 퀸을 놓고 싶은 행(인덱스)
for(int i=1; i<x; i++) { // 이전 행들을 체크
// 이전 행에서 퀸의 위치(열)가 새로 놓고자 하는 행에서 퀸의 위치(열)과 같음 혹은 대각선임
if(arr[i]==arr[x] || Math.abs(arr[x]-arr[i])==x-i) {
return false;
}
}
return true;
}
public static void nqueen(int x) {
c++;
if(check(x)) { // 1행은 일단 무조건 true라 먼저 놓고, 나머지 행들은 일단 넣고 체크함.
if(x==n) { // 방금 넣어서 체크 통과한 애가 마지막 애였던 거임.
cnt++;
}
else { // x는 행, i는 열
for(int i=1; i<=n; i++) { // (1,1~5) (2,1~5)
arr[x+1]=i;
nqueen(x+1); // (1)
}
}
}
}
}
Java
복사
각 경우 구하는 코드
2) 백준 N과 M문제 시리즈 정리(순열과 조합)
N과 M문제들은 백트래킹을 연습해보기 좋은 문제들이다.
백트래킹 기본 구조
nCr, nPr 등의 경우
1.
종료 조건 : r개의 수를 골랐을 때
2.
반복문 : 총 n개의 자연수
3.
제한 조건 : 이미 사용한 수는 사용 X
4.
상태 변화 : 사용한 수는 표시
5.
다음 단계 : 한 개의 수 더 고름
6.
원상 복구 : 사용했다고 표시한 거 복구
백트래킹 기본 틀
백트래킹 응용 틀
순열과 조합 → {1,2,3,4} n=4, r=2
•
순열 nPr : 서로 다른 n개 중에 r개를 선택하는 경우의 수 (순서 다르면 다르게 봄. 인정함)
{1,2} {1,3} {1,4}  {2,1} {2,3} {2,4}
{2,1} {2,3} {2,4}  {3,1} {3,2} {3,4}
{3,1} {3,2} {3,4}  {4,1} {4,2} {4,3}
{4,1} {4,2} {4,3}
N과 M(1), N과 M(5)
•
조합 nCr : 서로 다른 n개 중에 r개를 선택하는 경우의 수 (순서 달라도 하나로 봄. 인정 안함)
{1,2} {1,3} {1,4}  {2,3} {2,4}
{2,3} {2,4}  {3,4}
{3,4}
N과 M(2), N과 M(6)
•
중복순열 nπr : 중복 가능한 n개 중에 r개를 선택하는 경우의 수 (순서 다르면 다르게 봄)
{1,1} {1,2} {1,3} {1,4}  {2,1} {2,2} {2,3} {2,4}
{2,1} {2,2} {2,3} {2,4}  {3,1} {3,2} {3,3} {3,4}
{3,1} {3,2} {3,3} {3,4}  {4,1} {4,2} {4,3} {4,4}
{4,1} {4,2} {4,3} {4,4}
N과 M(3), N과 M(7) (특이사항: 출력할 때 시간 단축해줌)
•
중복조합 nHr : 중복 가능한 n개 중에 r개를 선택하는 경우의 수 (순서 달라도 하나로 봄)
{1,1} {1,2} {1,3} {1,4}  {2,2} {2,3} {2,4}
{2,2} {2,3} {2,4}  {3,3} {3,4}
{3,3} {3,4}  {4,4}
{4,4}
N과 M(4), N과 M(8)
같은 것이 있는 순열과 조합 → {1,1,1,2} n=4, r=4
•
순열 (순서 다르면 다르게 봄)
{1,1,1,2} {1,1,2,1} {1,2,1,1} {2,1,1,1}
N과 M(9)
•
조합 (순서 달라도 하나로 봄)
{1,1,1,2}
N과 M(10)
•
중복순열 (순서 다르면 다르게 봄)
{1,1,1,1} {1,1,1,2} {1,1,2,1} {1,1,2,2} {1,2,1,1} {1,2,1,2} {1,2,2,1} {1,2,2,2} {2,1,1,1} {2,1,1,2} {2,1,2,1} {2,1,2,2} {2,2,1,1} {2,2,1,2} {2,2,2,1} {2,2,2,2}
◦
1 네 개 2 네 개 있는데, 8P4하는 느낌
N과 M(11)
•
중복조합 (순서 달라도 하나로 봄)
{1,1,1,1} {1,1,1,2} {1,1,2,2} {1,2,2,2} {2,2,2,2}
◦
1 네 개 2 네 개 있는데, 8C4하는 느낌
N과 M(12)
3. 완전탐색 vs 백트래킹 → 문제 풀이 Tip
•
일단 완전탐색으로 풀었을 때의 시간 복잡도를 계산한 후
◦
가능할 거 같다면 한 번 풀어보고,
◦
시간초과가 날 거 같다면 백트래킹을 시도하기