1. 퍼셉트론에서 신경망으로
1) 신경망
•
정의) 여러 층으로 구성되고, 시그모이드 함수 등 매끈한 활성화 함수를 사용하는 네트워크
•
특징)
◦
가중치 매개변수의 적절한 값을 데이터로부터 자동 학습하는 능력 있음
▪
비교) 퍼셉트론: 가중치 설정은 사람이 수동으로 해야 함
◦
다층 퍼셉트론이 신경망 가리킴
▪
비교) 단순 퍼셉트론: 계단 함수를 활성화 함수로 사용한 모델
•
비교) 퍼셉트론과 다른 점: 구조 & 신호 전달 방식은 같음. 활성화 함수가 다름
◦
신경망
신경망 구조: ex) 2층 신경망
◦
퍼셉트론
퍼셉트론 구조
퍼셉트론 수식
퍼셉트론 수식 간결하게 변형 → 중간에 활성화 함수 사용
3) 활성화 함수의 등장
•
정의) h(x)와 같이 입력 신호의 총합을 출력 신호로 변환하는 함수
◦
입력 신호의 총합이 활성화를 일으키는지(1 또는 0) 정함
•
특징)
그림: 퍼셉트론에서 편향과 활성화 함수 처리 과정을 명시함
◦
퍼셉트론에서 신경망으로 가기 위한 길잡이
2. 활성화 함수
1) 계단 함수 → 단순 퍼셉트론
•
정의) 임계값을 경계로 출력이 바뀌는 함수
◦
입력이 0을 넘으면 1출력, 0 안 넘으면 0 출력
•
특징)
◦
그래프가 계단 형태임
◦
퍼셉트론에서는 활성화 함수로 계단 함수를 이용함
▪
계단 함수말고 다른 함수 쓰면 신경망이 될 수 있음
•
구현)
코드: x가 실수(부동소수점)만 받아들임. 넘파이 못 받아들임.
코드: 넘파이 지원하도록 수정함
•
그래프)
코드: plotting
실행 결과(그림)
2) 시그모이드 함수 → 신경망(다층 퍼셉트론)
•
정의)
•
특징)
◦
그래프가 s자 모양임
◦
신경망에선 활성화 함수로 시그모이드 함수를 자주 이용함
▪
시그모이드 함수로 변환한 신호를 다음 뉴런에 전달
•
구현)
코드
•
그래프)
코드: plotting
실행 결과(그림)
3) 시그모이드 함수와 계단 함수 비교
•
공통점
◦
크게 보면 같은 모양임 (구조)
▪
입력이 작을 때 출력이 0에 가깝고 (입력이 중요치 않으면 작은 값 출력)
▪
입력이 클 때 출력이 1에 가까움 (입력이 중요하면 큰 값 출력)
◦
출력이 0에서 1사이임
◦
비선형 함수임
▪
직선 1개로는 그릴 수 없는 함수
▪
신경망은 비선형 함수만 사용함(선형이면 층 나누는 의미 없어져서)
•
자세히는 책보고 더쓰기(p73)
•
차이점
◦
시그모이드 함수
▪
실수 반환
•
뉴런 사이에 연속적인 실수가 흐름
▪
매끄러움. 부드러운 곡선 형태
•
입력에 따라 출력이 연속적으로 변화함
◦
계단 함수
▪
0 또는 1 반환
•
뉴런 사이에 0 또는 1이 흐름 (흐르거나 흐르지 않거나)
▪
매끄럽지 않음. 계단(구부러진 직선) 형태
•
경계에서 출력이 갑자기 바뀜
3. 다차원 배열의 계산
1) 다차원 배열
•
정의) 숫자를 N차원으로 나열한 것. 한 줄로 나열이 아니라 여러 줄로 나열.
•
구현)
코드: 1차원 배열
코드: 다차원 배열 (2차원 배열)
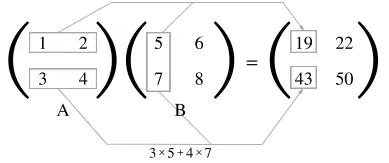
2) 2차원 배열(행렬)의 곱
•
정의) 앞 행렬의 행과 뒷 행렬의 열을 원소 별로 곱한 후 이를 더한 값을 원소로 하여 새로운 배열 만듦
•
구현)
코드 (2*2행렬과 2*2행렬의 곱)
코드 (2*3행렬과 3*2행렬의 곱)
코드 (2*2행렬과 2*3행렬의 곱) → 에러
코드 (3*2행렬과 1차원 배열의 곱)
•
특징)
◦
앞 행렬의 열 수(1번째 차원의 원소 수)와 뒷 행렬의 행 수(0번째 차원의 원소 수)가 같아야 함. 형상이 서로 반대.
▪
ex) 2*3 행렬과 3*2 행렬 곱 가능
대응하는 차원의 원소 수 일치해야 함.
3) 신경망에서의 행렬 곱
•
정의) 행렬의 곱으로 신경망 계산을 수행함
•
구현) 편향과 활성화 함수 생략하고 가중치만 갖는 신경망
코드
그림
4. 3층 신경망 구현
•
3층 신경망
◦
정의) 입력층(0층), 첫 번째 은닉층(1층), 두 번째 은닉층(2층), 출력층(3층)
그림
•
표기법
◦
정의) 은닉층 뉴런과 가중치의 표기법
▪
가중치
•
위: 층 (ex. 1 → 1층의 가중치)
•
밑: 다음 층 번호, 앞 층 번호 (ex. 3 2 → 0층의 2번째 누런에서 1층의 3번째 누런으로 감)
▪
뉴런
•
위: 층 (ex. 1 → 1층의 뉴런)
•
밑: 해당 층에서 번호 (ex. 3 → 3번째 뉴런)
그림) 입력층 → 은닉층
•
각 층의 신호 전달 구현
◦
예시) 입력층에서 1층으로의 신호 전달. 편향 추가.
▪
특징
•
1층의 첫 번째 뉴런으로의 가는 경우
•
편향은 한 층에 하나라서 앞 층 번호 표시 안 하고 다음 층 번호만 표시
•
입력 신호, 가중치, 편향은 적당한 값으로 설정함
그림
수식) 행렬 곱으로 간소화
코드
◦
예시) 1층에서 2층으로의 신호 전달. 활성화 함수 추가.
▪
특징
•
2층의 두 번째 뉴런으로 가는 경우
•
활성화 함수로 시그모이드 함수 사용함
그림
코드
◦
예시) 2층에서 출력층으로의 신호 전달
▪
특징
•
출력층의 첫 번째 뉴런으로 감
•
출력층의 활성화함수는 항등 함수를 사용함
•
항등함수: 입력을 그대로 출력하는 함수. (시그마라고 읽음)
그림
코드
•
3층 신경망 구현 정리
◦
출력층의 활성화 함수
▪
회귀 → 항등 함수
▪
2클래스 분류 → 시그모이드 함수
▪
다중 클래스 분류 → 소프트맥스 함수
코드
5. 출력층 설계
1) 분류와 회귀
•
분류
◦
정의) 데이터가 어느 클래스에 속하느냐의 문제
◦
예시) 사진 속 인물의 성별 분류 문제
◦
특징) 소프트맥스 함수 사용
◦
??: logistic regression
•
회귀
◦
정의) 입력 데이터에서 (연속적인) 수치를 예측하는 문제
◦
예시) 사진 속 인물의 몸무게(55.5kg?)를 예측하는 문제
◦
특징) 항등 함수 사용
2) 항등 함수
•
정의) 입력을 그대로 출력하는 함수
•
특징) 회귀에서 사용
그림
3) 소프트맥스 함수
•
정의) 확률값 출력하는 함수
◦
입력 신호의 지수함수 모든 입력 신호의 지수함수의 합
◦
n: 출력층의 뉴런 수
◦
: k번째 출력
•
특징)
◦
분류에서 사용
◦
출력은 확률임
▪
출력이 0에서 1.0사이의 실수임. 출력의 총합은 1임
▪
ex) y[0]의 확률 0.018(1.8%), y[1]의 확률 0.245(24.5%), y[2]의 확률 0.737(73%_
•
2번째 원소의 확률이 가장 높으니, 답은 2번째 클래스
▪
소프트맥스 함수 적용해도 원소의 대소관계는 변함 없음
•
이유) 지수함수가 단조 증가함수라서
•
신경망을 이용한 분류는 가장 큰 출력 내는 뉴런에 해당하는 클래스로 인식함
◦
결론) 신경망으로 분류할 때는 출력층의 소프트맥스 함수 생략해도 됨
◦
정확히는 추론 단계에선 생략하고, 학습 단계에선 사용함
▪
학습과 추론
•
학습: 모델을 학습
•
추론: 앞서 학습한 모델로 미지의 데이터에 대해 추론(분류) 수행
그림) 출력이 모든 입력 신호로부터 영향 받음
•
구현
코드
◦
구현 시 주의점
▪
오버플로우 문제
•
정의) 지수 함수 값이 너무 큰데, 너무 큰 값은 표현할 수 없음
지수함수 그래프
코드(오버플로우 문제 발생)
•
해결)
수식
코드(오버플로우 문제 해결)
4) 출력층의 뉴런 수 정하기
•
정의) 출력층의 뉴런 수는 풀려는 문제에 맞게 적절히 정함
◦
분류에선 분류하고 싶은 클래스 수로 설정
▪
ex. 0~9 숫자 중 하나로 분류 → 출력층 뉴런 10개
그림
6. 손글씨 숫자 인식
•
신경망의 문제 해결 과정
1.
학습) 훈련 데이터(학습 데이터) 사용해 가중치 매개변수를 학습
2.
추론) 앞서 학습한 매개변수 사용해 입력 데이터를 분류
1) MNIST data set
•
정의) 손글씨 숫자 분류의 데이터
•
특징)
◦
0~9까지의 숫자 이미지 데이터
◦
훈련 이미지 60000장
▪
훈련 이미지 사용해 모델 학습
◦
시험 이미지 10000장
▪
학습한 모델로 시험 이미지들 분류
◦
각 이미지는 28*28 크기. 각 픽셀에서 0~255까지의 값 취함
◦
실제 의미하는 숫자가 각 이미지에 레이블로 붙어있음
•
사용
◦
MNIST 데이터 셋 내려받아 이미지를 넘파이 배열로 변환한 파이썬 파일 mnist.py를 임포트해 사용
◦
mnist.py의 load_mnist()함수 사용하면 MNIST 데이터 쉽게 가져올 수 있음
코드) MNIST 데이터 가져옴
◦
load_mnist()함수의 인자
▪
normalize : 입력 이미지의 픽셀 값을 0.0~1.0 사이 값으로 정규화할지 결정
•
False → 입력 이미지 픽셀을 원래 값 그대로 0~255 사이 값으로 유지
▪
flatten : 입력 이미지를 평탄하게, 즉 1차원 배열로 만들지 결정
•
False → 입력 이미지를 1*28*28의 3차원 배열로 저장
•
True → 입력 이미지를 784개 원소로 이뤄진 1차원 배열로 저장
▪
one_hot_label : 원-핫 인코딩 형태로 저장할지 결정
•
원-핫 인코딩: [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] 처럼 정답 뜻하는 원소만 1이고, 나머진 0인 배열
•
False → 7, 2 와 같이 숫자 형태의 레이블 저장
•
True → 레이블을 원-핫 인코딩하여 저장
코드) MNIST 데이터 이미지 보기 → 첫 번째 훈련 이미지 보기
2) 신경망의 추론 처리
•
정의) MNIST 데이터셋으로 추론 수행하는 신경망 구현
•
특징)
◦
입력층 뉴런: 784개
◦
출력층 뉴런: 10개
◦
은닉층: 2개
▪
첫 번째 은닉층: 50개 뉴런 배치 (50,100은 임의로 정함)
▪
두 번째 은닉층: 100개 뉴런 배치
•
구현
코드) 신경망에 의한 추론, 정확도 평가
3) 배치 처리
•
정의) 하나로 묶은 입력 데이터
•
예시) 이미지 100개를 한번에 묶어 predict()함수에 한번에 넘김
◦
이미지 1개씩 넘길 때 형상
◦
이미지 100개씩 넘길 때 형상
•
구현)
코드