•
정의) 사이클이 없는 방향 그래프에서 에지로 주어진 노드 간 선후관계를 위배하지 않도록 나열하는 정렬
◦
사이클이 없는 방향 그래프(DAG: Directed Acyclic Graph)에서 노드 순서를 찾는 알고리즘
◦
진입 차수 배열을 이용한 정렬
•
활용)
◦
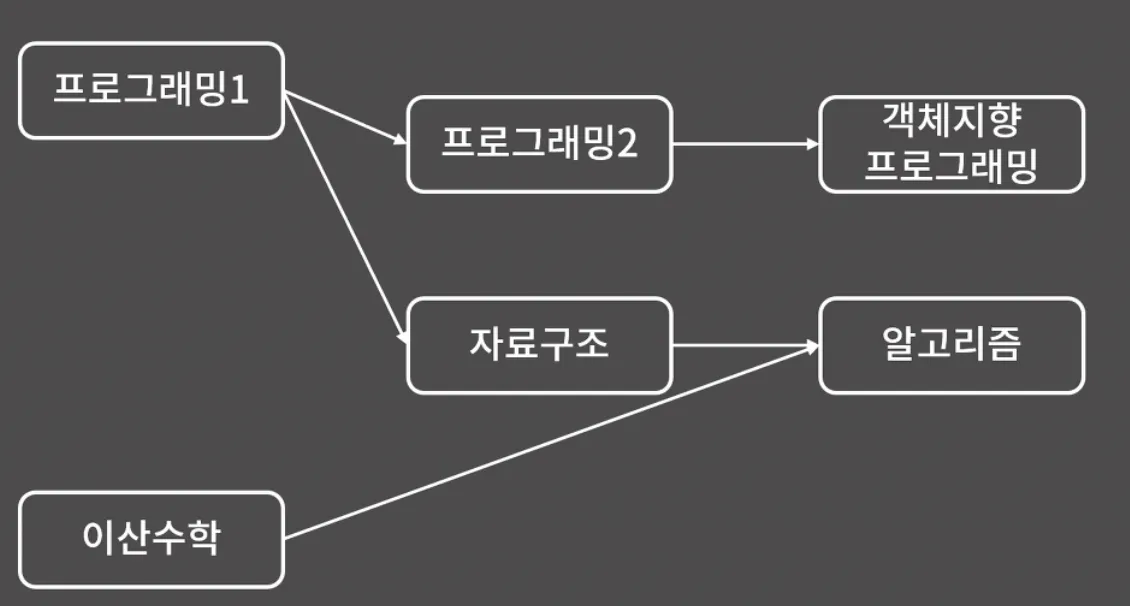
선수 과목이 있는 교과 이수 제도에서 모든 과목을 수강하기 위한 수강 순서 찾기 → 정답 여러 개
▪
이산→프1→프2→자구→객체→알골
▪
프1→프2→객체→자구→이산→알골
▪
자구에서 알골로 향하는 에지가 있으므로 위상 정렬을 했을 때 자구는 알골보다 앞에 등장해야 함
•
특징)
◦
노드 간의 순서를 결정함
◦
사이클이 없어야 함 → 사이클이 존재하면 노드 간의 순서를 명확하게 정렬할 수 없기 때문
◦
시간 복잡도 : O(V+E) (V:노드 수, E: 에지 수)
◦
항상 유일한 값으로 정렬되지 않아 정답이 여러 개일 수 있음
◦
맨 앞에 오려면 자신에게 들어오는 에지가 없어야 한단 점에 착안
◦
dfs 순회 결과를 뒤집은 것이 위상 정렬 결과
•
추상화한 과정)
1.
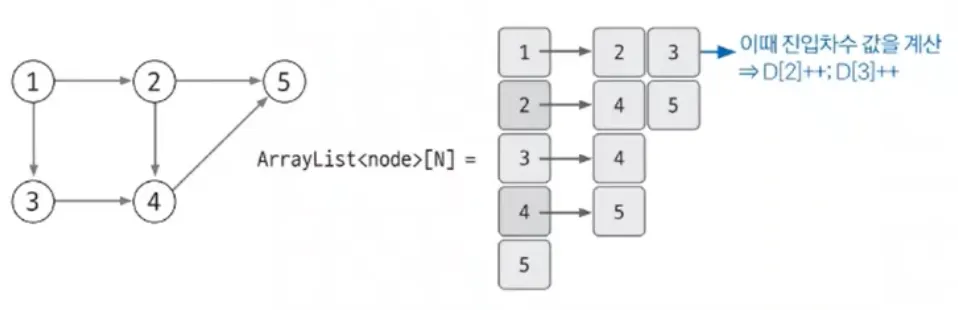
그래프를 인접리스트 형태로 구현하면서 실시간으로 진입 차수 값을 계산해 진입 차수 배열을 함께 생성
•
진입 차수(in-degree): 자기 자신을 가리키는(들어오는) 에지의 개수
•
진출 차수(out-degree): 자기에게서 나가는 에지의 개수
2.
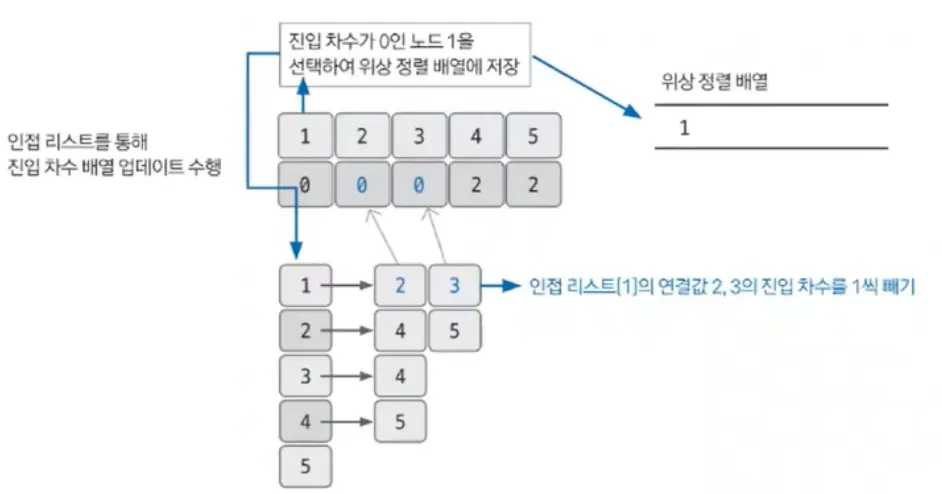
진입 차수 배열에서 진입 차수가 0인 노드를 선택하고, 선택된 노드를 정렬 결과 배열에 저장함. 그 후, 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 1씩 뺌
•
정렬한 노드(1)가 가리키는 노드(2,3)들의 진입 차수를 1씩 빼는 이유: 1이 등장한 후엔 “2와 3은 1보다 먼저 등장할 수 없다”라는 제약 조건이 의미가 없어졌기 때문. 즉 간선의 의미가 없어졌기에, 노드 1과 노드 1에서 뻗어나가는 간선을 지워버리는 것과 같은 효과를 주는 거임.
3.
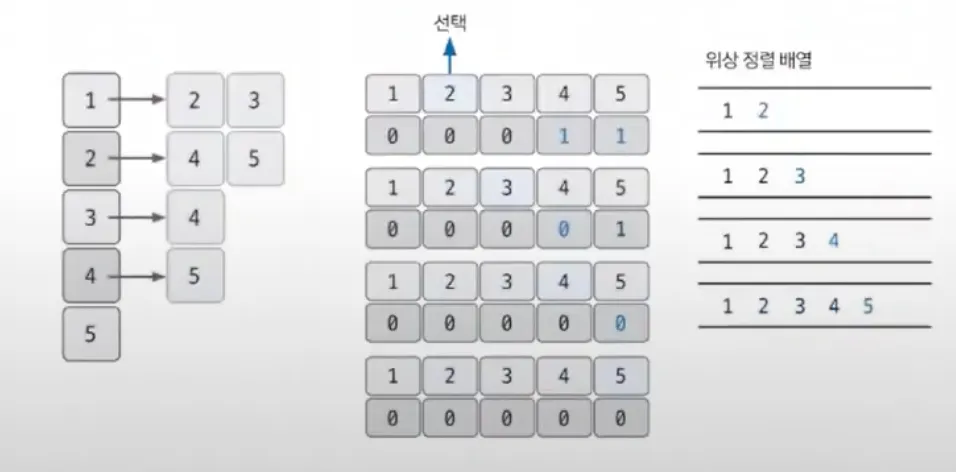
사용한 노드는 더이상 사용하지 않고, 남은 노드 대상으로 2번을 반복. 모든 노드가 정렬될 때까지 반복
•
진입 차수가 0인 노드가 여러 개일 수 있고, 어떤 것을 선택하든 정답이기에 위상 정렬이 늘 같은 정렬 결과를 보장하지 않는다 한 것임
4.
위상 정렬 결과에 모든 정점이 포함되어 있는지 확인해 사이클 여부 확인. 모든 정점이 포함되어 있다면 사이클이 없는 것.
•
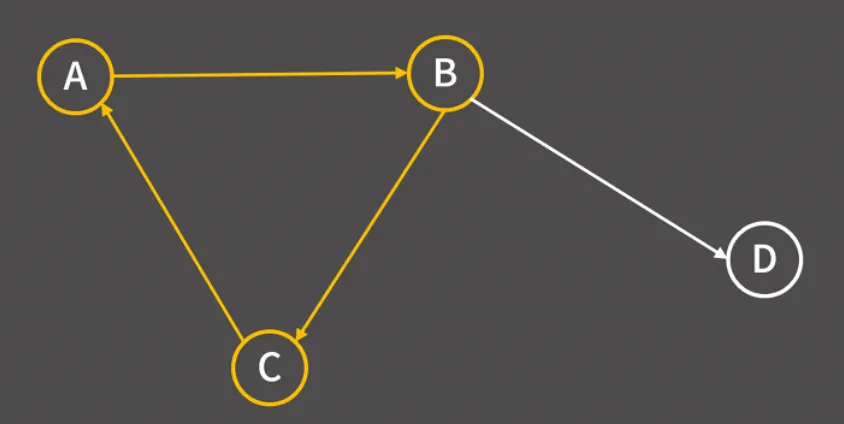
A, B, C 어느 것도 진입 차수가 0이 될 수 없음. A의 진입 차수가 0이 되려면 B의 진입 차수가 0이 되어 선택되어야 하는데, B의 진입 차수가 0이 되려면 C의 진입 차수가 0이 되어 선택되어야 하고, C의 진입 차수가 0이 되려면 A의 진입 차수가 0이 되어야 하기 때문에 A, B, C는 서로 물고 물려있음. 따라서 사이클에 포함된 노드들은 절대 정렬 결과에 들어갈 수 없음
•
구체화한 과정)
1.
그래프를 인접리스트로 표현하면서 진입차수배열 초기화
2.
진입차수가 0인 노드들을 큐에 넣기
3.
큐에서 뺀 노드를 정렬 결과에 넣고, 해당 노드가 가리키는 노드들의 진입차수 값을 1씩 빼기
•
1을 뺐을 때 진입차수가 0이 된 노드는 큐에 넣기
4.
큐가 빌 때까지 3을 반복
5.
개수로 비교했을 때 정렬 결과에 모든 노드가 들어가지 않았다면, 사이클 존재하는 것이니 예외 처리
•
코드)
// n : 노드 수, m : 에지 수, numbers : 에지 목록 (ex. 0 1 / 1 2 -> 1에 0과 2가 연결됨)
private static int[] solution(int n, int m, int[][] numbers) {
// 1. 그래프를 인접리스트로 표현하면서 진입차수배열 초기화
ArrayList<Integer>[] graph = new ArrayList[n + 1];
int[] inDegree = new int[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
graph[numbers[i][0]].add(numbers[i][1]);
inDegree[numbers[i][1]]++;
}
// 2. 진입차수가 0인 노드들을 큐에 넣기
Queue<Integer> queue = new LinkedList<>();
for (int i = 1; i <= n; i++) {
if (inDegree[i] == 0) {
queue.add(i);
}
}
// 3~4. 큐에서 뺀 노드를 정렬 결과에 넣고, 해당 노드가 가리키는 노드들의 진입차수 값을 1씩 빼기. 이때, 진입 차수가 0이 된 노드는 큐에 넣기
ArrayList<Integer> result = new ArrayList<>();
while (!queue.isEmpty()) {
int targetNode = queue.poll();
result.add(targetNode);
for (int nearNode : graph[targetNode]) {
inDegree[nearNode]--;
if (inDegree[nearNode] == 0) {
queue.add(nearNode);
}
}
}
// 5. 개수로 비교했을 때 정렬 결과에 모든 노드가 들어가지 않았다면, 사이클 존재하는 것이니 예외 처리
if (result.size() != n) {
throw new IllegalArgumentException("사이클이 존재합니다");
}
return result.stream().mapToInt(i -> i).toArray();
}
Java
복사
참고