정의
•
그래프에서 모든 노드를 연결할 때 사용된 에지들의 가중치의 합을 최소로 하는 트리
용어
•
최소 신장 트리: 신장 트리 중 간선의 합이 최소인 트리
•
신장 트리: 그래프의 부분 그래프들 중 모든 정점을 포함하는 트리
•
부분 그래프: 주어진 그래프에서 일부 정점과 간선만을 택해서 구성한 새로운 그래프
•
트리: 무방향이면서 사이클이 없는 연결 그래프
특징
•
주로 크루스칼 알고리즘이나 프림 알고리즘으로 구현
◦
사이클 만들지 않는 선에서 비용이 작은 간선부터 최소신장트리에 편입시키는 그리디 알고리즘
•
사이클 있는지 판별하기 위해 유니온 파인드 사용해 구현
◦
유니온파인드 이용해 크루스칼 알고리즘 구현 시 시간 복잡도는 O(ElogE)
•
N개의 노드가 있으면 최소 신장 트리를 구성하는 에지의 개수는 항상 N-1개
◦
에지를 N개 이상 사용하면 사이클이 생김
◦
사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않음
•
동일한 그래프에서 최소 신장 트리 여러 개 존재할 수도 있음
◦
가중치 제일 작은 에지가 여러 개일 수도 있어서
과정: 크루스칼
1.
그래프를 에지 리스트로 구현하고, 유니온 파인드 리스트 초기화
•
유니온파인드는 인덱스를 해당 자리의 값으로 초기화하면 됨
2.
그래프 데이터를 가중치 기준으로 오름차순 정렬
3.
가중치가 낮은 에지부터 연결 시도
•
가중치 가장 낮은 에지가 여러 개라면 그 중 아무거나 택해도 상관 없음
•
연결 시도할 때 사이클이 되는지 확인해야 함 → 사이클 생기면 연결 하면 안됨
◦
두 노드에 대해 find 연산 수행했을 때 두 노드의 대표 노드가 같다면 사이클이 생긴단 의미
◦
사이클 생긴단 건, 이미 현재 에지보다 가중치 낮은 다른 에지들로 해당 노드가 연결되어 있단 거라서 연결 안함 → 최대한 적은 가중치로 노드들 연결하는 게 목적
4.
연결한 에지의 개수가 N-1이 될 때까지 과정 3을 반복 (N: 전체 노드의 개수)
5.
완성된 최소 신장 트리의 총 에지 비용 출력
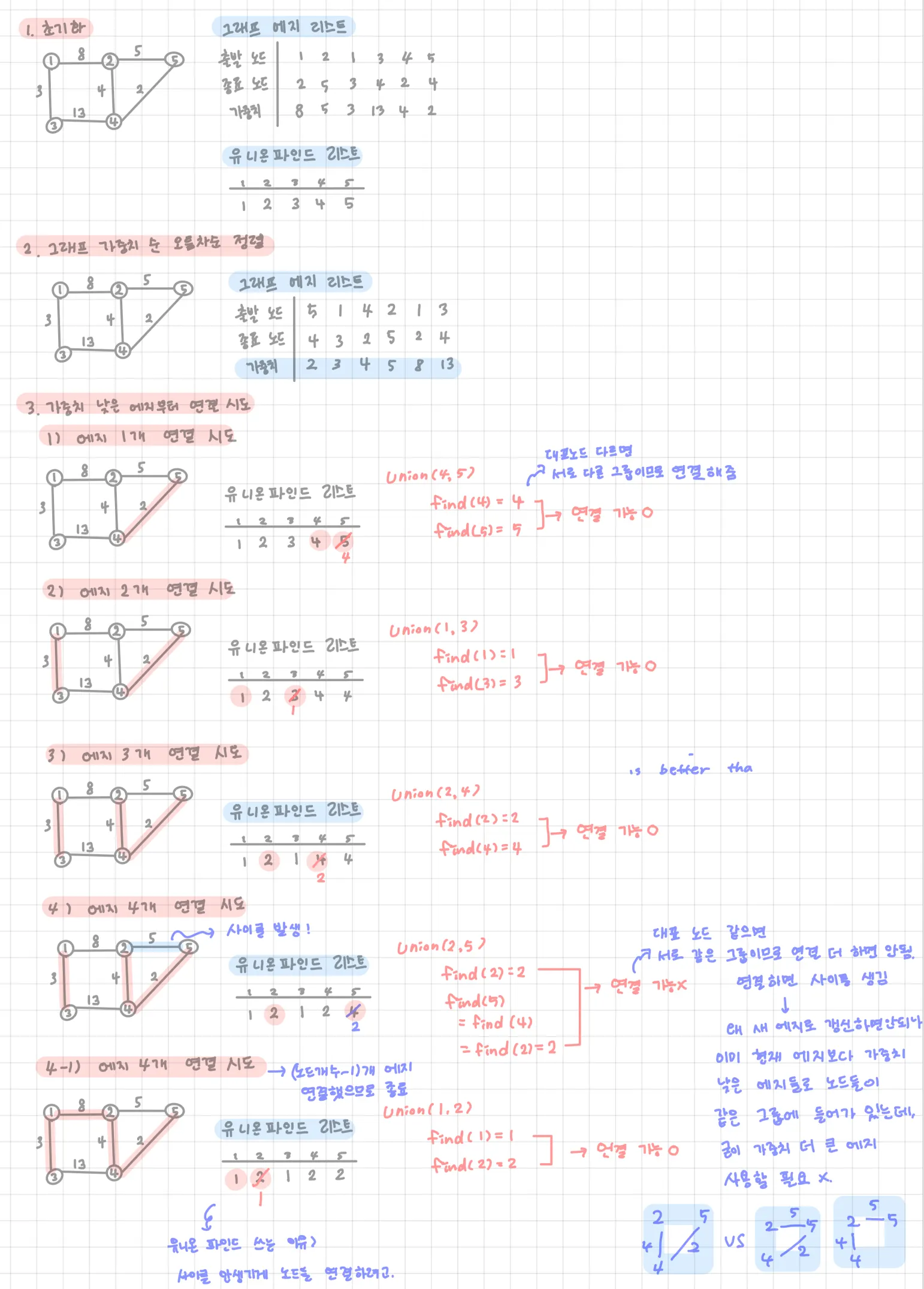
예시: 크루스칼
코드: 크루스칼
private static int[][] graph;
private static int[] unionfind;
private static int solution(int n, int m) {
// 1. 그래프 에지 리스트와 유니온 파인드 리스트 초기화
graph = new int[m][3];
for (int i = 0; i < m; i++) { // 주의할 점: 그래프 0번째 인덱스 안비워둠(정렬 때문에)
String input = br.readLine().split(" ");
graph[i][0] = Integer.parseInt(input[0]);
graph[i][1] = Integer.parseInt(input[1]);
graph[i][2] = Integer.parseInt(input[2]);
}
unionfind = new int[n + 1];
for (int i = 1; i <= n; i++) {
unionfind[i] = i;
}
// 2. 그래프 가중치 순 오름차순 정렬
Arrays.sort(graph, (s1, s2) -> {
return s1[2] - s2[2];
});
// 3. 가중치 낮은 에지부터 연결 시도
int index = 0;
int count = 0;
int weightSum = 0;
while (count < n - 1) { // 4. 연결한 에지의 개수가 N-1이 될 때까지 과정 3을 반복
int start = graph[index][0];
int end = graph[index][1];
int weight = graph[index++][2];
if (isSameGroup(start, end)) {
continue;
}
union(start, end);
count++;
weightSum += weight;
}
return weightSum; // 5. 완성된 최소 신장 트리의 총 에지 비용
}
Java
복사
참고