1. 병합 정렬 (Merge Sort)
•
정의) 분할정복 방식 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 알고리즘
◦
재귀적으로 수열을 나눠 정렬한 후 합치는 정렬법
•
특징)
◦
시간 복잡도 : 최선 O(NlogN) , 평균 O(NlogN) , 최악 O(NlogN)
▪
N번의 데이터 접근이 logN번 일어나므로 시간 복잡도가 NlogN임
◦
우선 순위가 같은 원소들끼리는 원래 순서 따라가는 안정 정렬(Stable Sort)임
◦
임시 배열에 정열한 결과를 저장해야 하기에 메모리많이 필요하단 단점 있음
•
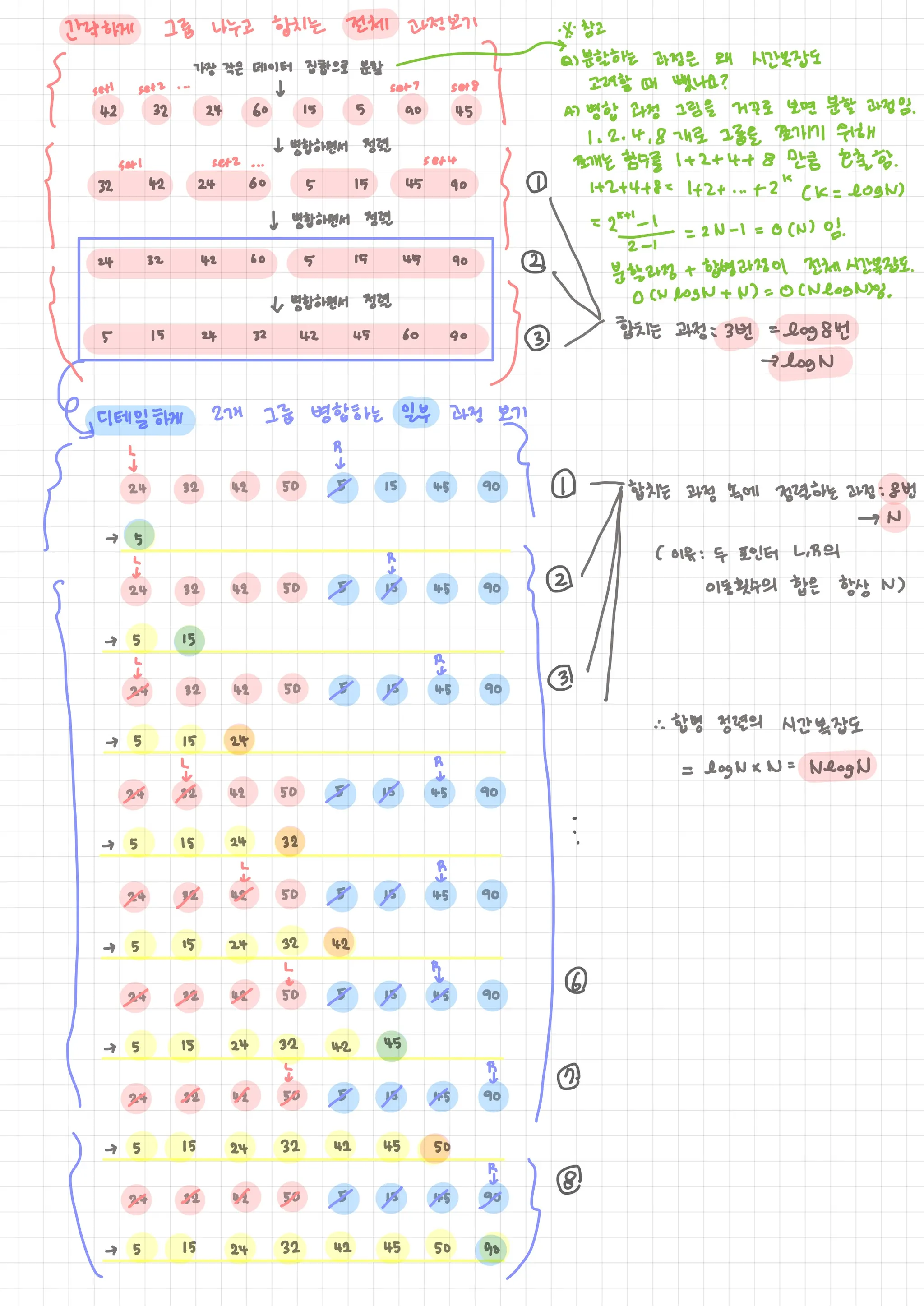
과정 간략하게) 그룹 나누고 합치는 전체 과정 (with 분할정복)
◦
가장 작은 데이터 집합으로 분할함
◦
병합하면서 정렬하는 걸 반복함
•
과정 상세히) 2개의 그룹을 병합하는 일부 과정 (중요) (with 투포인터)
1.
투포인터로 2개의 그룹 각각의 첫 번째 원소를 가르킴 (각 그룹이 정렬되어 있으므로 투포인터 사용 가능)
2.
첫 번째 그룹의 포인터(left)와 두 번째 그룹(right)의 포인터의 값을 비교해,
•
작은 값을 결과 배열에 추가하고,
•
해당 포인터를 오른쪽으로 한 칸 이동시킴
3.
2를 반복하다가 둘 중 한 그룹의 포인터가 마지막 원소까지 다 사용하고 범위 밖으로 나가면,
•
남아 있는 그룹의 모든 원소를 배열의 뒤에 추가해줌
•
예시)
•
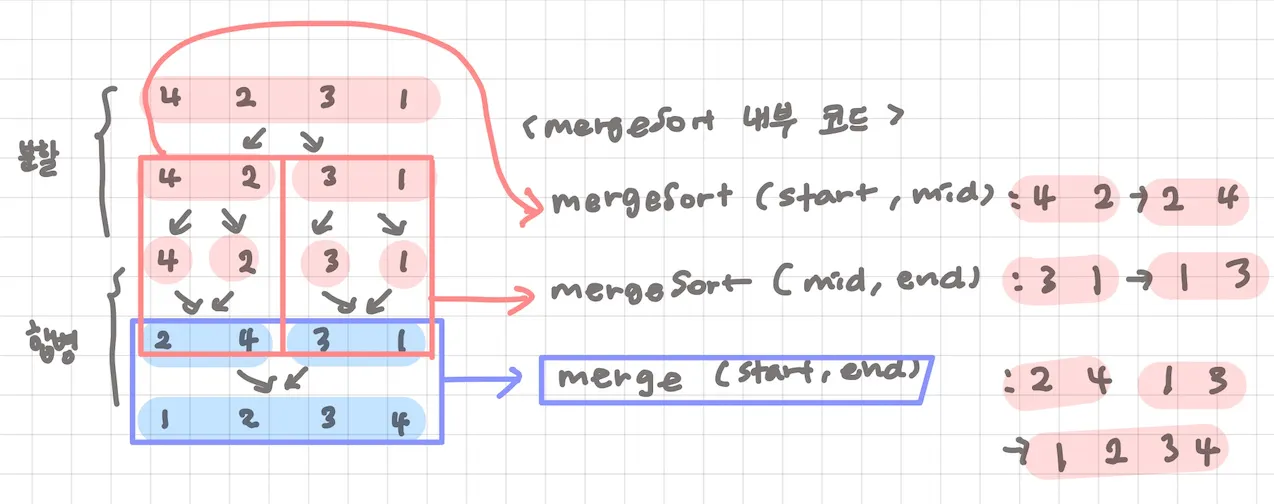
코드
private static int[] numbers; // main에서 초기화 (크기는 n)
private static int[] temp; // main에서 초기화 (크기는 n)
private static void solution(int n) { // numbers={5,4,1,2,3} -> n=5
mergeSort(0, n);
}
private static void mergeSort(int start, int end) {
if (end - start == 1) {
return;
}
int mid = (start + end) / 2;
mergeSort(start, mid);
mergeSort(mid, end);
merge(start, end);
}
private static void merge(int start, int end) {
int mid = (start + end) / 2;
int left = start;
int right = mid;
for (int i = start; i < end; i++) {
if (left == mid) {
temp[i] = numbers[right++];
} else if (right == end) {
temp[i] = numbers[left++];
} else if (numbers[left] <= numbers[right]) { // 합병 정렬의 안정 정렬 성질 만족시키기 위해서 크기 같을 땐 앞 쪽에 들어가게 해줌
temp[i] = numbers[left++];
} else {
temp[i] = numbers[right++];
}
}
for (int i = start; i < end; i++) {
numbers[i] = temp[i];
}
}
Java
복사
2. 기수 정렬 (Radix Sort)
•
정의) 값을 놓고 비교할 자릿수를 정한 다음 값이 아닌 해당 자릿수만 비교하는 정렬
•
특징)
◦
시간 복잡도 : O(kn) (k는 데이터의 자릿수)
◦
N개 데이터가 모두 자릿수가 같다면 한 리스트에 N개의 원소가 다 몰릴 것이기에 10개의 리스트 모두 N칸의 배열로 만들어야 함. 공간 낭비 크므로 동적 배열 혹은 연결 리스트 사용하는 게 좋음.
•
과정) 0~99 사이의 숫자일 때
◦
값의 자릿수를 대표하는 10개의 큐 준비
◦
일의 자릿수를 기준으로 한 큐에 데이터를 저장
◦
일의 자리에서 정렬된 순서 기준으로 데이터를 차례로 빼서 십의 자릿수를 기준으로 한 큐에 저장
◦
십의 자리에서 정렬된 순서 기준으로 데이터를 차례로 뺀 것이 정렬의 결과임
•
예시)
•
코드 1) 간편하게 기수 정렬 구현
private static int[] numbers; // 정렬 대상 수들
private static int[] powerOfTen = new int[5];
private static void initPowerOfTen() {
powerOfTen[0] = 1;
for (int i = 1; i < 5; i++) {
powerOfTen[i] = powerOfTen[i - 1] * 10;
}
}
private static int findDigitNum(int x, int a) {
return (x / powerOfTen[a]) % 10; // 10^a
}
private static void solution(int n, int maxSize) { // ex. 정렬 대상 수들이 최대 10000일 떄 -> solution(numbers.length, 5)
initPowerOfTen();
Queue<Integer>[] digitList = new LinkedList[10];
for (int i = 0; i < 10; i++) {
digitList[i] = new LinkedList<>();
}
for (int i = 0; i < maxSize; i++) {
for (int j = 0; j < 10; j++) {
digitList[i].clear();
}
for (int j = 0; j < n; j++) {
digitList[findDigitNum(numbers[j], i)].add(numbers[j]);
}
int numberIdx = 0;
for (int j = 0; j < 10; j++) {
while (!digitList[j].isEmpty()) {
numbers[numberIdx++] = digitList[j].remove();
}
}
}
}
Java
복사
•
코드 2) 기수 정렬의 메모리 부족 문제를 해결하고 싶다면 계수 정렬을 내부적으로 활용해 구현
◦
자릿수 별로 정렬할 때 계수 정렬을 활용. 원래 기수 정렬은 이런 식으로 계수 정렬의 한계를 극복하기 위해 나온 것임
◦
이 코드는 부분적으로 계수 정렬을 사용하긴 하지만, 전체적으론 결국 자릿수 별로 정렬한다는 기수 정렬의 정의에 부합하므로, 기수 정렬을 사용한 코드라고 보는 게 더 타당함
◦
기수 정렬을 구현할 때 내부적으로 사용하는 방식만 바뀐 것 뿐임
private static int[] numbers;
private static int[] powerOfTen = new int[5];
private static void initPowerOfTen() {
powerOfTen[0] = 1;
for (int i = 1; i < 5; i++) {
powerOfTen[i] = powerOfTen[i - 1] * 10;
}
}
private static int findDigitNum(int x, int a) {
return (x / powerOfTen[a]) % 10; // 10^a
}
private static void solution(int n, int maxSize) {
initPowerOfTen();
for (int i = 0; i < maxSize; i++) {
int[] temp = new int[n]; // 사실상 swap 느낌이라 temp 필요함
int[] bucket = new int[10];
for (int j = 0; j < n; j++) {
int digitNumber = findDigitNum(numbers[j], i);
bucket[digitNumber]++;
}
for (int j = 1; j < bucket.length; j++) {
bucket[j] += bucket[j - 1]; // 구간합
}
for (int j = n - 1; j >= 0; j--) {
int digitNumber = findDigitNum(numbers[j], i);
int tempIdx = bucket[digitNumber] - 1;
temp[tempIdx] = numbers[j];
bucket[digitNumber]--;
}
for (int j = 0; j < n; j++) {
numbers[j] = temp[j];
}
}
}
Java
복사
4. 비교 함수
•
특징)
◦
a가 b의 앞에 와야 할 때 true를, 그렇지 않을 때에는 false를 반환
◦
a와 b 두 값이 같을 땐 반드시 false를 반환
참고