1. 정렬 알고리즘
•
정의) 데이터를 특정한 조건에 따라 일정한 순서가 되도록 다시 배열하는 일
•
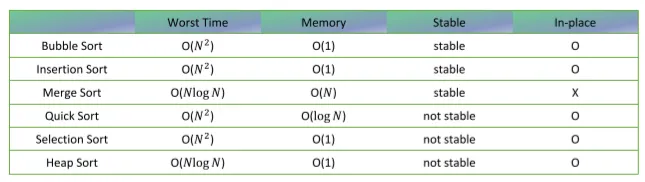
분류)
◦
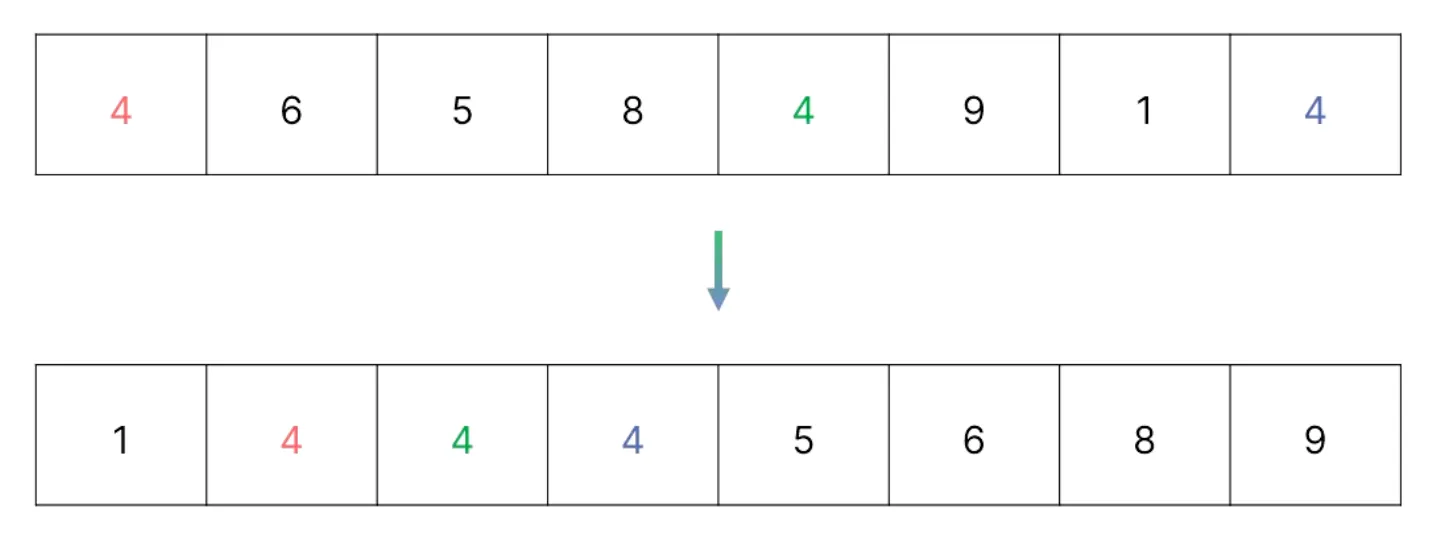
안정 정렬(Stable Sort) : 동일한 값들은 정렬 전의 위치 유지
▪
버블 정렬, 삽입 정렬, 합병 정렬
◦
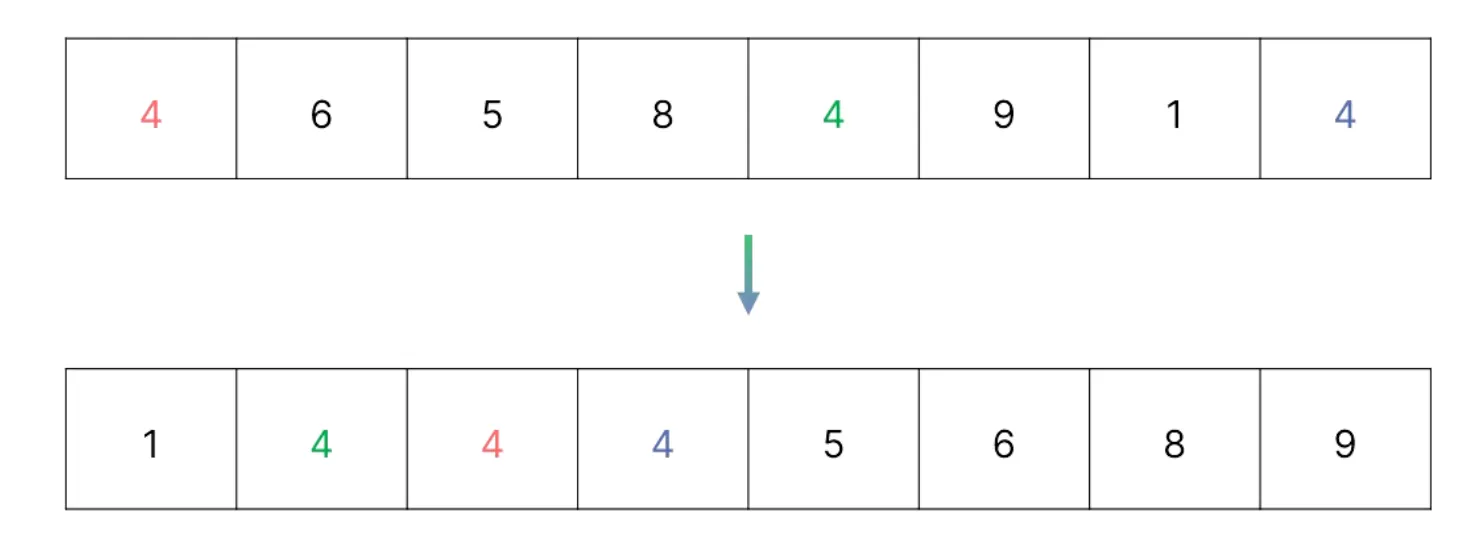
불안정 정렬(Unstable Sort) : 동일한 값들이 정렬 후 순서가 바뀜
▪
퀵 정렬, 선택 정렬, 힙 정렬
◦
불안정 정렬 : 동일한 값들이 정렬 후 순서가 바뀜
▪
퀵 정렬, 선택 정렬, 힙 정렬
•
정리) 각각의 상황에 맞는 효율적인 방법 선택
2. 버블 정렬
•
정의)
◦
앞에서부터 두 개씩 보며 큰 수가 뒤로 가게끔 자리를 바꿔줌.
◦
위 알고리즘을 배열에 아무 변화가 없을 때까지 반복함.
▪
i가 같을 때 swap 한 번도 안 한 경우
•
예시) 6 5 3 8
◦
5 6 3 8 → i=0, j=0
◦
5 3 6 8 → i=0, j=1
◦
5 3 6 8 → i=0, j=2
◦
3 5 6 8 → i=1, j=0
◦
3 5 6 8 → i=1, j=1
◦
3 5 6 8 → i=2, j=0
•
특징)
◦
매번 반복할 때마다 가장 큰 수가 제일 뒤로 감
◦
시간 복잡도 : 최선 O(N) , 평균 O(N^2) , 최악 O(N^2)
•
코드)
void bubbleSort (int[] arr) {
int n = arr.length; // n=4
for(int i = 0; i < n-1; i++) { // i=0,j=0~2 / i=1,j=0~1 / i=2,j=0
for(int j = 0; j < n-1-i; j++) {
if (arr[j] > arr[j+1]) // 큰 게 앞에 있다면
swap(arr[j], arr[j+1]); // 자리 바꿔서 큰 걸 뒤로 보내기
}
}
}
Java
복사
3. 삽입 정렬
•
정의)
◦
이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입하여 정렬시키는 방식
•
과정)
◦
k번째 원소를 앞의 원소들과 역순으로 비교하며,
▪
처음으로 등장하는 본인보다 크지 않은(작거나 같은) 원소 뒤에 위치시킴
◦
위 알고리즘을 배열에 아무 변화가 없을 때까지 반복함
•
예시) 6 5 3 8
◦
i=1, j=0 → key=5 → 5 6 3 8
◦
i=2, j=1 → key=3 → 3 5 6 8
◦
i=3, j=2 → key=8 → 3 5 6 8
•
특징)
◦
매번 반복할 때마다 앞의 배열이 정렬됨
◦
시간 복잡도 : 최선 O(N) , 평균 O(N^2) , 최악 O(N^2)
◦
적절한 삽입 위치를 정렬된 부분에서 탐색하는 부분에서 이진 탐색 등과 같은 탐색 알고리즘을 사용해 시간 복잡도 줄일 수 있음
▪
그럼에도 시간 복잡도가 좋을 수 없는 이유는, 찾는 건 빨리 해서 O(N)을 O(logN)으로 줄였다고 하더라도 삽입할 뒷 부분의 데이터들에 대해 shift 연산을 수행해야 하는데 이 shift 연산이 시간이 많이 걸리기 때문임
•
코드)
void insertionSort(int[] arr) {
int n = arr.length; // n=4
for (int i = 1; i < n; i++) { // i=1~3
int key = arr[i]; // 앞의 원소들과 역순 비교할 원소
int j = i - 1; // 비교대상의 인덱스. i=1,j=0 / i=2,j=1 / i=3,j=2
while(j >= 0 && arr[j] > key) {// 앞의 원소가 key보다 크고, j가 0이상이면 반복
arr[j + 1] = arr[j]; // 적어도 arr[j]보단 앞으로 삽입될 것이기에, 그 뒤는 한 칸씩 미뤄주기 (참고로, 밀리는 값들이 들어갈 자리의 맨 뒤는 key의 자리라서 사실상 swap임)
j = j - 1;
}
arr[j + 1] = key; // 앞의 원소가 key보다 작거나 같은 상황이 나오면, 그 뒤에 위치시킴
}
}
Java
복사
4. 선택 정렬
•
정의) 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방식
•
과정)
◦
정렬 안 된 부분에서 최소값 또는 최대값을 찾고, 정렬 안 된 부분의 가장 앞에 있는 데이터와 swap
◦
위 과정을 반복함
•
예시) 4 3 1 2
◦
1 3 4 2 → {1}은 정렬 확정
◦
1 2 4 3 → {1,2}은 정렬 확정
◦
1 2 3 4 → {1,2,3,4}은 정렬 확정
•
특징)
◦
매번 반복할 때마다 가장 작은 수가 제일 앞으로 감 (오름차순 정렬 기준)
◦
시간 복잡도 : 최선 O(N^2), 평균 O(N^2) , 최악 O(N^2)
•
코드)
void selectionSort (int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
Java
복사
5. 퀵 정렬
•
정의) 기준값(pivot)을 선정해 해당값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 방식
◦
매 단계마다 피벗이라고 이름 붙은 원소 하나를 제자리로 보내는 작업을 반복하는, 재귀적으로 구현되는 정렬
◦
여기서 제자리로 보낸다는 의미는 피벗의 왼쪽은 피벗보다 작은 원소가, 오른쪽은 큰 원소가 오게 하는 것
•
과정 간략하게)
◦
임의의 index를 피벗(pivot)으로 잡음
◦
피벗 좌측에는 피벗보다 작은 수, 우측에는 큰 수가 오게끔 배치함
◦
피벗을 제외한 피벗의 좌측과 우측 두 개의 리스트에 대해서 위 과정을 재귀적으로 반복함 (분할정복)
•
예시)
•
과정 상세히)
1.
데이터를 분할하는 피벗을 설정 (예시의 경우 가장 오른쪽 끝을 피벗으로 설정)
2.
피벗을 기준으로 아래 과정을 거쳐 2개의 집합으로 분리함 (포인터로 잘못된 위치에 있는 값 찾아나감)
a.
start가 가리키는 데이터가 피벗이 가리키는 데이터보다 작으면 start를 오른쪽으로 한 칸 이동
(피벗보다 큰 애가 나오면 멈춤. 그 자리가 아니라서 나중에 swap 해주기 위해)
b.
end가 가리키는 데이터가 피벗이 가리키는 데이터보다 크면 end를 왼쪽으로 한 칸 이동
(피벗보다 작은 애가 나오면 멈춤. 그 자리가 아니라서 나중에 swap 해주기 위해)
c.
start, end가 가리키는 데이터를 swap 하고 start는 오른쪽, end는 왼쪽으로 한 칸씩 이동
d.
end가 start보다 작아질 때까지 a~c를 반복
e.
pivot과 end를 swap
3.
분리 집합에서 각각 다시 pivot을 선정
4.
분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복
•
특징)
◦
시간 복잡도 : 최선 O(NlogN) , 평균 O(NlogN) , 최악 O(N^2)
◦
기준값이 어떻게 선정되는지가 시간 복잡도에 많은 영향을 미침
▪
피벗으로 계속 최대값이거나 최소값을 선택한다면, 좌우측으로 넘길 때 전부다 판단해야 하기 때문에 최악이 O(N^2)임
•
예시) 1 2 3 4 5 100 에서 100이 피벗이라면,
◦
end는 5로 그대로고 start가 1부터 5까지 다훑고 올라와서 start와 end가 5에서 만남
◦
결국 100은 다시 5 뒷자리에 들어가 원래 상태 그대로 유지임
▪
피벗으로 중간 정도 크기의 숫자 택하는 게 중요함. 좌우측으로 반반 분할정복이 가능해짐(up down 게임처럼). 물론 중간 정도 크기의 숫자가 어디에 있는지 알 방법은 없기에 운에 따름.
•
pivot이 매번 완벽하게 중앙에 위치해서 리스트를 균등하게 둘로 쪼갠다면 단계의 개수가 logN이 될 테고, 각 단계마다 pivot을 제자리로 보내는 데에 O(N)이 필요해서 총 O(NlogN)이 나옴
•
pivot이 매번 어느 정도로만 잘 자리잡는다면 시간복잡도는 여전히 O(NlogN)임. 심지어 매번 리스트를 1:99의 배율로 쪼개더라도 마찬가지임
◦
STL을 못 쓰고 직접 정렬을 구현해야 하는 상황에서 다른 정렬을 선택할 수 있다면 퀵 소트는 절대 쓰지 말고, 머지 소트나 힙 소트 같은 다른 O(NlogN)인 정렬을 쓸 것
▪
머지 소트가 퀵 소트보다 느린 건 맞지만 어차피 O(NlogN)에 돌아가니 충분히 빠름. 이에 반해, 퀵 소트는 최악의 경우 O(N^2)이라 쓸 필요가 없기 때문임
▪
그럼에도, 대부분의 라이브러리에선 퀵 소트를 씀. 라이브러리에선 피벗을 랜덤하게 택하기도 하고, 피벗 후보를 3개 정해서 그 3개 중 중앙값을 피벗으로 두기도 한는 등 다양한 처리를 함.
▪
또, 최악의 경우에도 O(NlogN)을 보장하기 위해서 일정 깊이 이상 들어가면 퀵 소트 대신 힙 소트로 정렬함. 이러한 정렬을 Introspective sort라 부름.
•
장점)
◦
추가적인 공간이 필요하지 않음 (추가적인 공간을 사용하지 않는 정렬 == In-Place Sort)
◦
배열 안에서의 자리 바꿈만으로 처리 되기 때문에 cache hit rate 가 높아서 속도가 빠름
•
단점)
◦
리스트가 오름차순이거나 내림차순일 때는 시간복잡도로 O(N^2)이 나옴
•
코드)
static int[] numbers = new int[1_000_001];
private static void quickSort(int start, int end) {
if (end <= start + 1) {
return;
}
int pivot = numbers[start];
int left = start + 1;
int right = end - 1;
while (true) {
while (left <= right && numbers[left] <= pivot) {
left++;
}
while (left <= right && numbers[right] >= pivot) {
right--;
}
if (left > right) {
break;
}
swap(left, right);
}
swap(start, right);
quickSort(start, right);
quickSort(right + 1, end);
}
private static void swap(int i, int j) {
int temp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = temp;
}
public static void main(String[] args) throws Exception {
System.setIn(new java.io.FileInputStream("res/input.txt"));
java.util.Scanner sc = new java.util.Scanner(System.in);
int n = sc.nextInt();
for (int i = 0; i < n; i++) {
numbers[i] = sc.nextInt();
}
quickSort(0, n);
for (int i = 0; i < n; i++) {
System.out.println(numbers[i] + " ");
}
sc.close();
}
Java
복사
6. 병합 정렬 (Merge Sort)
•
정의) 분할정복 방식 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 알고리즘
◦
재귀적으로 수열을 나눠 정렬한 후 합치는 정렬법
•
특징)
◦
시간 복잡도 : 최선 O(NlogN) , 평균 O(NlogN) , 최악 O(NlogN)
▪
N번의 데이터 접근이 logN번 일어나므로 시간 복잡도가 NlogN임
◦
우선 순위가 같은 원소들끼리는 원래 순서 따라가는 안정 정렬(Stable Sort)임
◦
임시 배열에 정열한 결과를 저장해야 하기에 메모리많이 필요하단 단점 있음
•
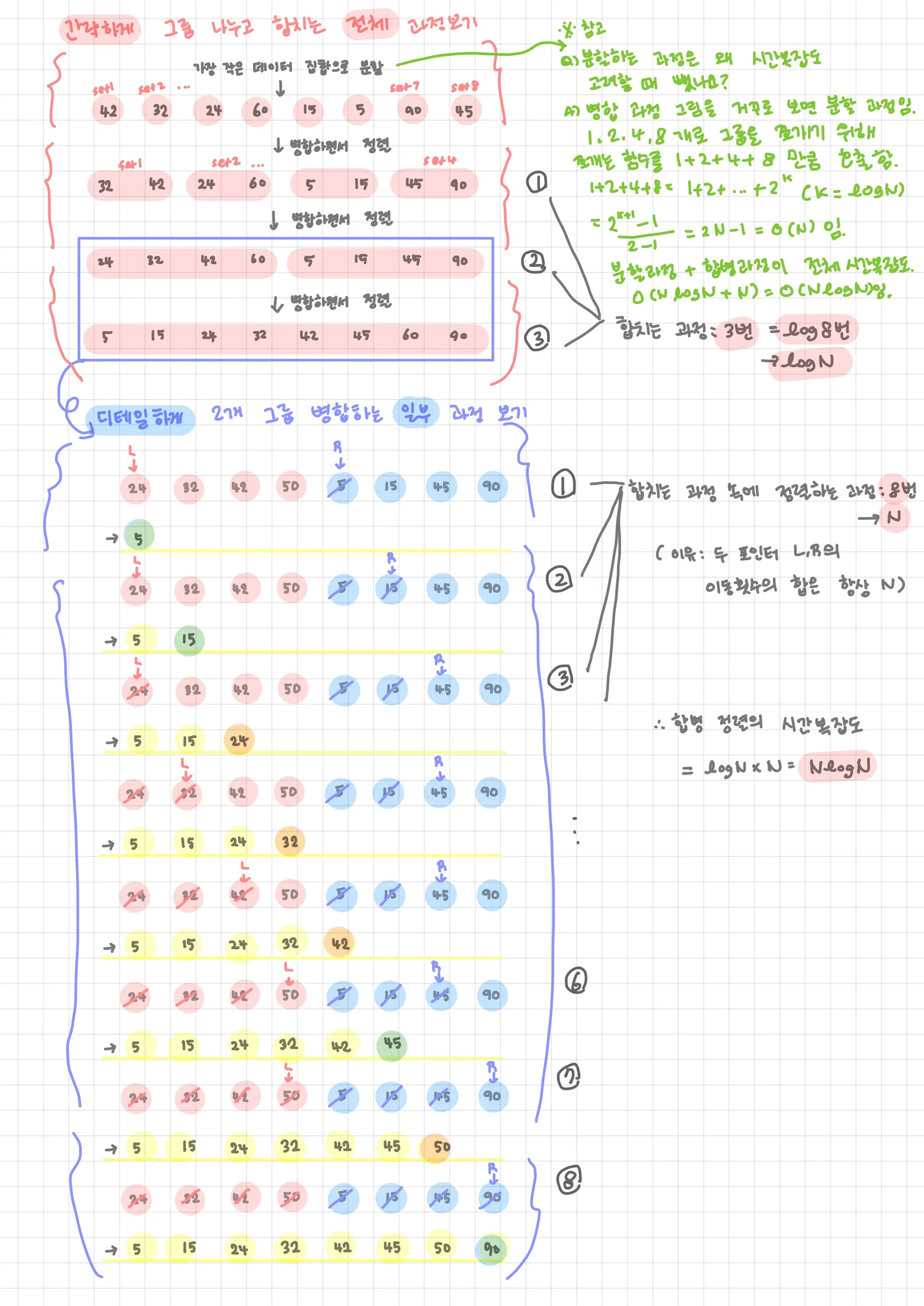
과정 간략하게) 그룹 나누고 합치는 전체 과정 (with 분할정복)
◦
가장 작은 데이터 집합으로 분할함
◦
병합하면서 정렬하는 걸 반복함
•
과정 상세히) 2개의 그룹을 병합하는 일부 과정 (중요) (with 투포인터)
1.
투포인터로 2개의 그룹 각각의 첫 번째 원소를 가르킴 (각 그룹이 정렬되어 있으므로 투포인터 사용 가능)
2.
첫 번째 그룹의 포인터(left)와 두 번째 그룹(right)의 포인터의 값을 비교해,
•
작은 값을 결과 배열에 추가하고,
•
해당 포인터를 오른쪽으로 한 칸 이동시킴
3.
2를 반복하다가 둘 중 한 그룹의 포인터가 마지막 원소까지 다 사용하고 범위 밖으로 나가면,
•
남아 있는 그룹의 모든 원소를 배열의 뒤에 추가해줌
•
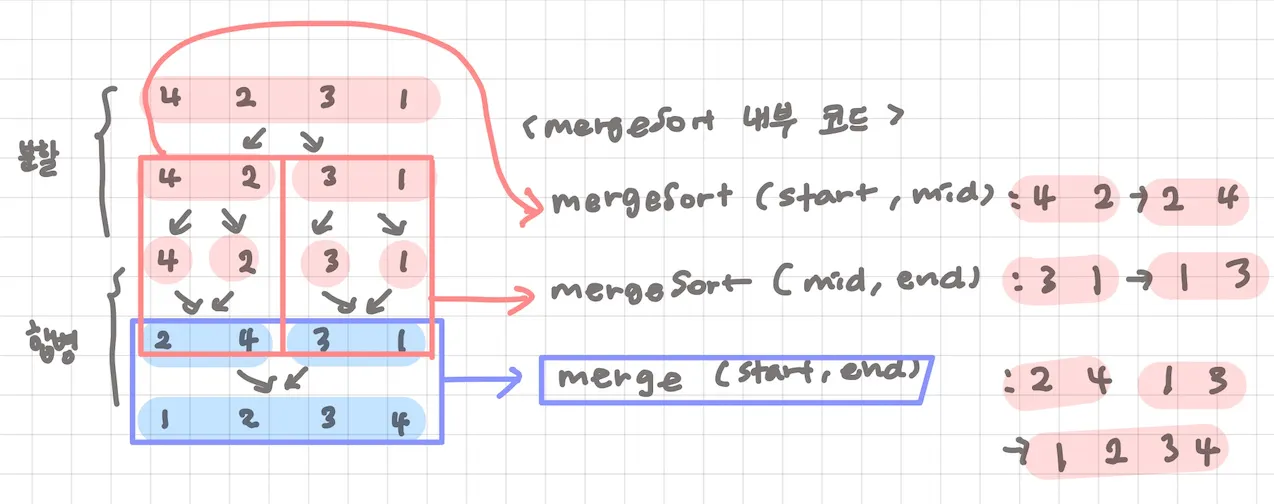
예시)
•
코드
private static int[] numbers; // main에서 초기화 (크기는 n)
private static int[] temp; // main에서 초기화 (크기는 n)
private static void solution(int n) { // numbers={5,4,1,2,3} -> n=5
mergeSort(0, n);
}
private static void mergeSort(int start, int end) {
if (end - start == 1) {
return;
}
int mid = (start + end) / 2;
mergeSort(start, mid);
mergeSort(mid, end);
merge(start, end);
}
private static void merge(int start, int end) {
int mid = (start + end) / 2;
int left = start;
int right = mid;
for (int i = start; i < end; i++) {
if (left == mid) {
temp[i] = numbers[right++];
} else if (right == end) {
temp[i] = numbers[left++];
} else if (numbers[left] <= numbers[right]) { // 합병 정렬의 안정 정렬 성질 만족시키기 위해서 크기 같을 땐 앞 쪽에 들어가게 해줌
temp[i] = numbers[left++];
} else {
temp[i] = numbers[right++];
}
}
for (int i = start; i < end; i++) {
numbers[i] = temp[i];
}
}
Java
복사
7. 기수 정렬 (Radix Sort)
•
정의) 값을 놓고 비교할 자릿수를 정한 다음 값이 아닌 해당 자릿수만 비교하는 정렬
•
특징)
◦
시간 복잡도 : O(kn) (k는 데이터의 자릿수)
◦
N개 데이터가 모두 자릿수가 같다면 한 리스트에 N개의 원소가 다 몰릴 것이기에 10개의 리스트 모두 N칸의 배열로 만들어야 함. 공간 낭비 크므로 동적 배열 혹은 연결 리스트 사용하는 게 좋음.
•
과정) 0~99 사이의 숫자일 때
◦
값의 자릿수를 대표하는 10개의 큐 준비
◦
일의 자릿수를 기준으로 한 큐에 데이터를 저장
◦
일의 자리에서 정렬된 순서 기준으로 데이터를 차례로 빼서 십의 자릿수를 기준으로 한 큐에 저장
◦
십의 자리에서 정렬된 순서 기준으로 데이터를 차례로 뺀 것이 정렬의 결과임
•
예시)
•
코드 1) 간편하게 기수 정렬 구현
private static int[] numbers; // 정렬 대상 수들
private static int[] powerOfTen = new int[5];
private static void initPowerOfTen() {
powerOfTen[0] = 1;
for (int i = 1; i < 5; i++) {
powerOfTen[i] = powerOfTen[i - 1] * 10;
}
}
private static int findDigitNum(int x, int a) {
return (x / powerOfTen[a]) % 10; // 10^a
}
private static void solution(int n, int maxSize) { // ex. 정렬 대상 수들이 최대 10000일 떄 -> solution(numbers.length, 5)
initPowerOfTen();
Queue<Integer>[] digitList = new LinkedList[10];
for (int i = 0; i < 10; i++) {
digitList[i] = new LinkedList<>();
}
for (int i = 0; i < maxSize; i++) {
for (int j = 0; j < 10; j++) {
digitList[i].clear();
}
for (int j = 0; j < n; j++) {
digitList[findDigitNum(numbers[j], i)].add(numbers[j]);
}
int numberIdx = 0;
for (int j = 0; j < 10; j++) {
while (!digitList[j].isEmpty()) {
numbers[numberIdx++] = digitList[j].remove();
}
}
}
}
Java
복사
•
코드 2) 기수 정렬의 메모리 부족 문제를 해결하고 싶다면 계수 정렬을 내부적으로 활용해 구현
◦
자릿수 별로 정렬할 때 계수 정렬을 활용. 원래 기수 정렬은 이런 식으로 계수 정렬의 한계를 극복하기 위해 나온 것임
◦
이 코드는 부분적으로 계수 정렬을 사용하긴 하지만, 전체적으론 결국 자릿수 별로 정렬한다는 기수 정렬의 정의에 부합하므로, 기수 정렬을 사용한 코드라고 보는 게 더 타당함
◦
기수 정렬을 구현할 때 내부적으로 사용하는 방식만 바뀐 것 뿐임
private static int[] numbers;
private static int[] powerOfTen = new int[5];
private static void initPowerOfTen() {
powerOfTen[0] = 1;
for (int i = 1; i < 5; i++) {
powerOfTen[i] = powerOfTen[i - 1] * 10;
}
}
private static int findDigitNum(int x, int a) {
return (x / powerOfTen[a]) % 10; // 10^a
}
private static void solution(int n, int maxSize) {
initPowerOfTen();
for (int i = 0; i < maxSize; i++) {
int[] temp = new int[n]; // 사실상 swap 느낌이라 temp 필요함
int[] bucket = new int[10];
for (int j = 0; j < n; j++) {
int digitNumber = findDigitNum(numbers[j], i);
bucket[digitNumber]++;
}
for (int j = 1; j < bucket.length; j++) {
bucket[j] += bucket[j - 1]; // 구간합
}
for (int j = n - 1; j >= 0; j--) {
int digitNumber = findDigitNum(numbers[j], i);
int tempIdx = bucket[digitNumber] - 1;
temp[tempIdx] = numbers[j];
bucket[digitNumber]--;
}
for (int j = 0; j < n; j++) {
numbers[j] = temp[j];
}
}
}
Java
복사
8. 비교 함수
•
특징)
◦
a가 b의 앞에 와야 할 때 true를, 그렇지 않을 때에는 false를 반환
◦
a와 b 두 값이 같을 땐 반드시 false를 반환