벨만포드
정의
•
하나의 시작 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘
특징
•
다익스트라와 다르게 음수 가중치 에지가 있어도 수행 가능
•
전체 그래프에서 음수 사이클의 존재 여부 판단하는 데에 사용 가능
•
에지를 중심으로 동작함
•
시간 복잡도 : O(VE) (V: 노드 수, E: 에지 수)
◦
노드 개수 - 1 번 만큼 에지들 전부 확인하는 작업 진행해서
과정
1.
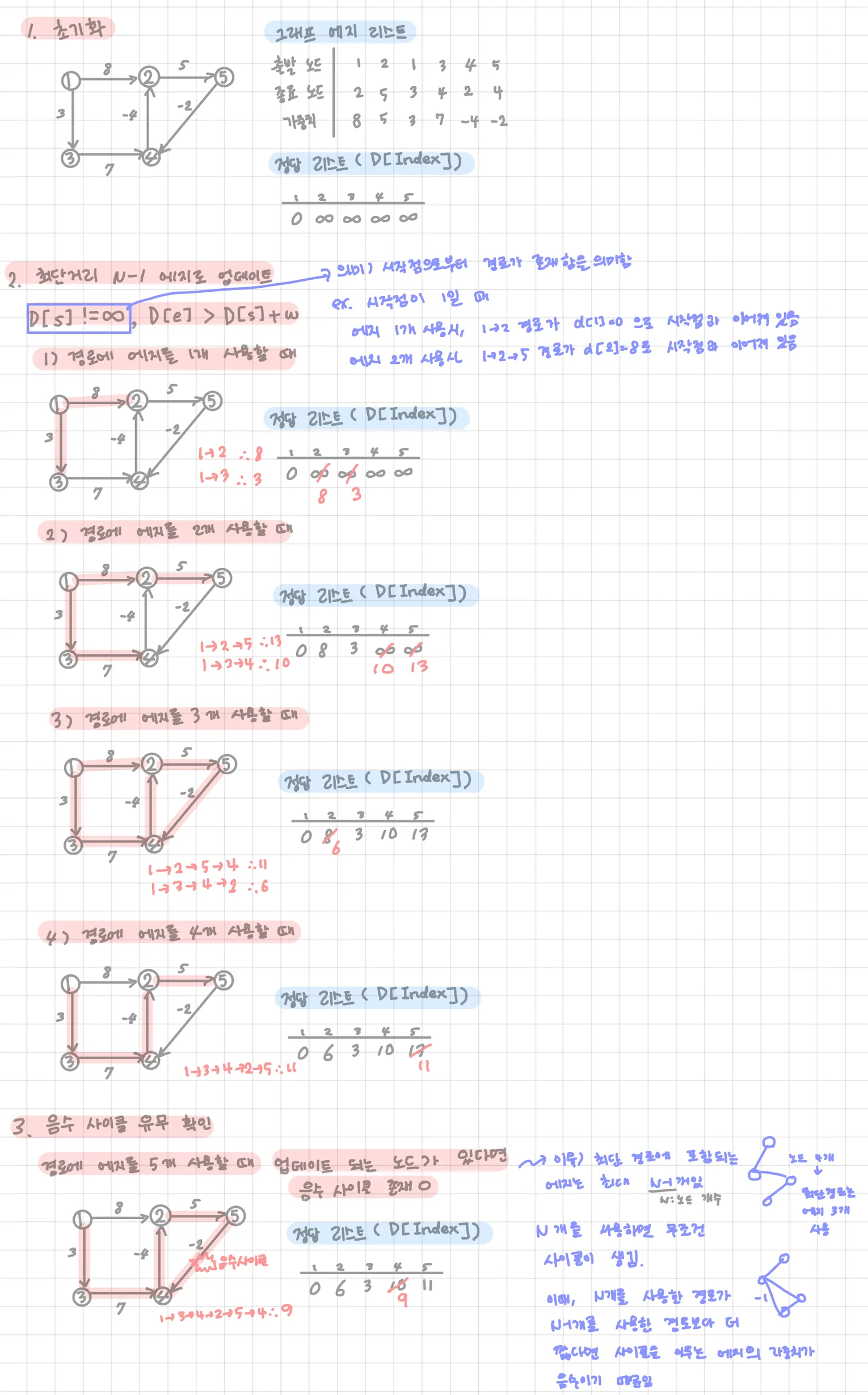
그래프를 에지 리스트로 구현하고, 최단 경로(정답) 리스트를 출발 노드는 0, 나머지는 무한대로 초기화하기
2.
모든 에지를 확인해 정답 리스트 업데이트하기
•
업데이트 조건: D[s]≠무한대 && D[e]>D[s]+w 일 때, D[e]를 D[s]+w로 업데이트
•
업데이트의 반복 횟수: 노드 개수 - 1
◦
노드 개수가 n이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 n-1이기 때문
◦
업데이트의 반복 횟수가 k번 이라면 해당 시점에 최단 경로 리스트의 값은 시작점에서 k개의 에지를 사용했을 때 각 노드에 대한 최단 거리를 의미함
3.
음수 사이클 유무 확인하기
•
모든 에지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하면 음수 사이클이 있단 의미
◦
음수 사이클이 있다면 2단계에서 도출한 정답 리스트가 무의미하고 최단 거리를 찾을 수 없는 그래프라는 뜻이 됨
◦
음수 사이클이 있다면 이 사이클을 무한하게 돌수록 가중치가 계속 감소해서 최단 거리를 구할 수 없음
예시
코드 (with 백준 11657)
private static final int START = 1;
private static final int INFINITE = 99_999_999;
private static String solution(int n, int m) { // n: 노드 수 m: 에지 수
// 1. 그래프를 에지 리스트로 표현하고, 최단거리 리스트(0,무한대) 초기화
int[][] numbers = new int[m + 1][3];
for (int i = 1; i <= m; i++) {
String input = br.readLine().split(" ");
numbers[i][0] = Integer.parseInt(input[0]);
numbers[i][1] = Integer.parseInt(input[1]);
numbers[i][2] = Integer.parseInt(input[2]);
}
long [] distance = new long[n + 1];
Arrays.fill(distance, INFINITE);
distance[START] = 0;
// 2. 최단거리를 사용하는 에지 개수 점차 늘려가며 업데이트 (D[s]!=무한대 && D[e]>D[s]+w 일 때, D[s]+w로 업데이트)
for (int i = 1; i <= m; i++) { // 경로에 사용할 에지의 개수 : 1 ~ m개
// 위 반복문 한 번 돌 때마다 시작점에 연결되어 무한대가 아니게 갱신되는 뎁스가 1씩 증가함. 즉, 경로에 들어간 에지 개수가 1씩 증가함.
for (int j = 1; j <= m; j++) { // 경로에 들어갈 수 있는지 살펴볼 에지 번호
int start = numbers[j][0];
int end = numbers[j][1];
int weight = numbers[j][2];
if (distance[start] != INFINITE && distance[end] > distance[start] + weight) {
// 시작점과 연결되어 있고, 이전 경로보다 해당 에지를 사용한 경로가 더 최단 경로라면 업데이트
distance[end] = distance[start] + weight;
}
}
}
// 3. 음수 사이클 존재하는지 확인
boolean isMinusCycle = false;
for (int j = 1; j <= m; j++) {
int start = numbers[j][0];
int end = numbers[j][1];
int weight = numbers[j][2];
if (distance[start] != INFINITE && distance[end] > distance[start] + weight) {
isMinusCycle = true;
}
}
}
Java
복사
플로이드 워셜
정의
•
모든 노드 간에 최단 거리를 구하는 알고리즘
특징
•
음수 가중치 에지가 있어도 수행 가능 (음수 사이클은 x)
•
동적 계획법의 원리를 이용해 알고리즘에 접근
•
시간 복잡도: O(V^3) (V: 노드 수)
◦
총 V(K=1,2,…,V) 단계에 걸쳐 갱신이 이루어지고
◦
각 단계마다 총 V^2개의 모든 D[S][E] 값을 D[S][K]+D[K][E] 값과 비교하기 때문
•
원리: A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단 경로
◦
전체 경로의 최단 경로는 부분 경로의 최단 경로의 조합으로 이루어짐
◦
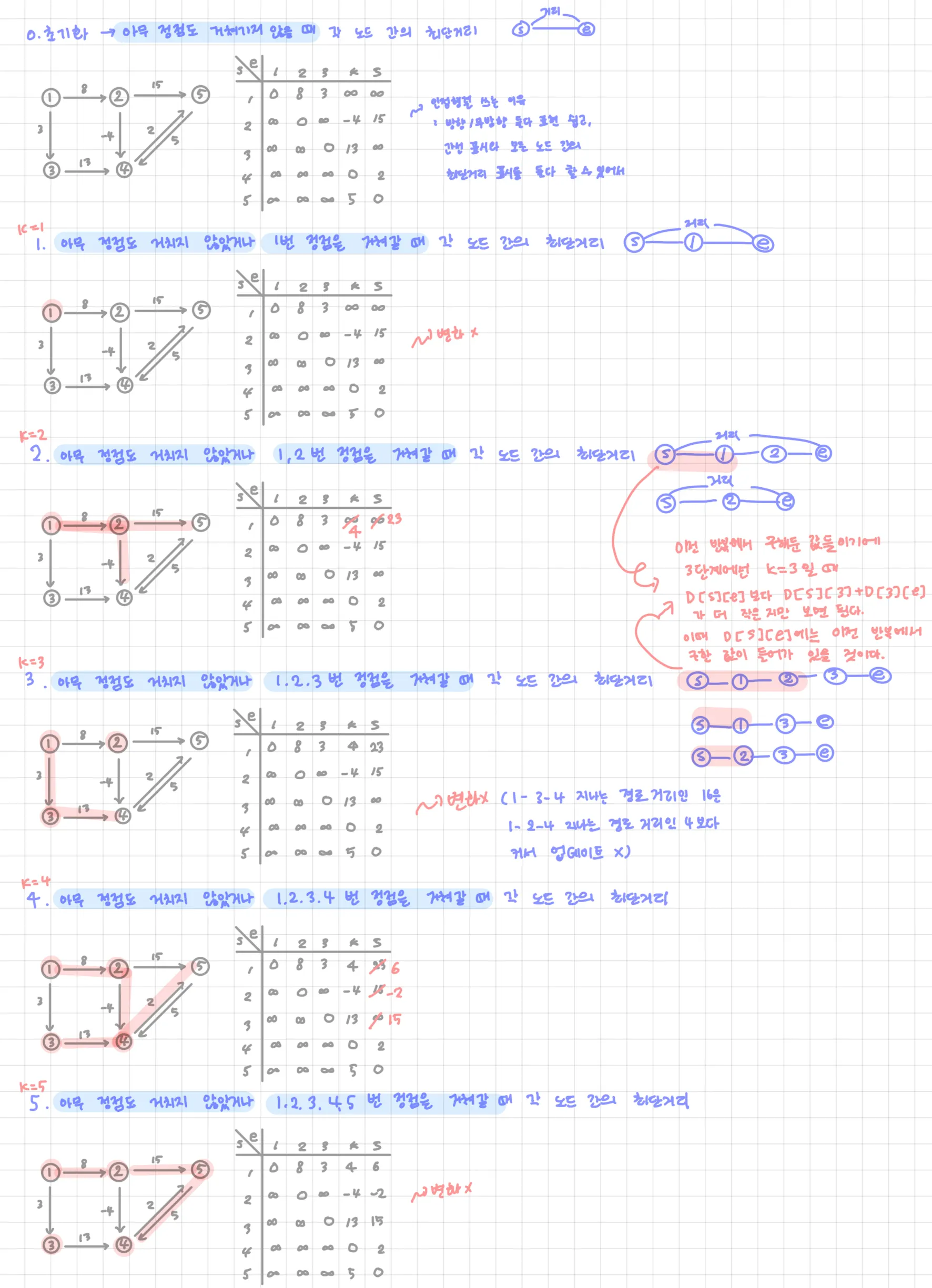
도출한 점화식: D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])
•
다른 관점에서 바라본 원리: 매 단계마다 특정 정점을 지나서 가는 걸 추가적으로 고려
◦
1단계를 거치고 나면 중간에 다른 정점을 거치지 않았거나 1번 정점을 거쳐서 갈 때의 최단 거리를 알 수 있고,
◦
2단계를 거치고 나면 중간에 다른 정점을 거치지 않았거나 1,2번 정점을 거쳐서 갈 때의 최단 거리를 알 수 있다는 식
•
그래프를 인접행렬(2차원 배열)로 표현해 구현 가능
과정
1.
최단 거리 저장
a.
리스트를 초기화
•
D[S][E]는 노드 S에서 노드 E까지의 최단 거리를 의미
•
S와 E의 값이 같은 값은 0, 다른 칸은 무한대로 초기화
2.
최단 거리 리스트에 그래프 데이터 저장
•
D[S][E] = W 로 에지의 가중치 정보를 리스트에 저장
3.
점화식으로 리스트 업데이트
•
점화식을 3중 for문의 형태로 반복하면서 리스트 값 업데이트
for 경유지 K에 관해 (1~N) # N: 노드 개수
for 출발 노드 S에 관해 (1~N)
for 도착 노드 E에 관해 (1~N)
D[S][E] = Math.min(D[S][E], D[S][k] + D[k][E])
Java
복사
예시
코드 (with 백준 11404)
private static int[][] solution(int n, int m, int[][] numbers) { // n: 노드 수, m: 에지 수
// 1-1. 최단 거리 저장하는 리스트에 기본 값으로(0,무한대) 초기화
int[][] distance = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
distance[i][j] = INF;
}
}
for (int i = 1; i <= n; i++) {
distance[i][i] = 0;
}
// 1-2. 최단 거리 리스트에 간선 정보 저장
for (int i = 0; i < m; i++) {
int s = numbers[i][0];
int e = numbers[i][1];
int w = numbers[i][2];
distance[s][e] = Math.min(distance[s][e], w);
}
// 2. 점화식으로 리스트 업데이트
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
distance[i][j] = Math.min(distance[i][j], distance[i][k] + distance[k][j]);
}
}
}
return distance;
}
Java
복사
참고