그래프
•
정의) 노드(정점)와 에지(간선)로 구성된 집합
•
용어)
◦
노드 : 데이터를 표현하는 단위
◦
에지 : 노드를 연결
◦
차수 : 각 노드에 대해서 에지로 연결된 이웃한 노드의 개수
•
종류)
◦
방향/무방향 그래프 : 방향성 유무에 따름, 방향성 있다는 건 일방통행 도로 같은 것
▪
방향 그래프에서 자기에게서 나가는 에지 개수를 outdegree, 들어오는 에지의 개수를 indegree라 부름
◦
순환/비순환 그래프 : 사이클 하나라도 있으면 순환, 사이클 하나도 없으면 비순환 그래프
▪
사이클 : 임의의 한 점에서 출발해 자기 자신으로 돌아올 수 있는 경로
◦
완전 그래프 : 모든 서로 다른 두 노드 쌍이 에지로 연결된 그래프
◦
연결 그래프 : 임의의 두 정점 사이에 경로가 항상 존재하는 그래프
◦
단순 그래프 : 두 정점 사이의 간선이 1개 이하이고 루프가 존재하지 않는 그래프
▪
루프 : 한 노드에서 시작해 같은 노드로 들어오는 에지
•
활용) 그래프에서 사용하는 알고리즘
◦
유니온 파인드 : 그래프의 사이클이 생성되는지 판별하는 알고리즘
◦
위상정렬 : 사이클이 없는 방향이 있는 그래프일 때, 그래프의 각 노드들을 선형으로 정렬
▪
예시) a → b → c, a → d 선형 정렬 시
•
a → b → c → d 또는 a → d → b → c
▪
특징)
•
결과값이 유일하지 않음
•
수강 신청(수1→수2) 같은 전후 관계가 명확히 있는 상황에 활용 (전후관계라는게 그래프에서의 방향을 의미하고, 전후관계 명확하려면 사이클 없어야 함)
◦
최단 거리 알고리즘 : 다익스트라, 벨만-포드, 플로이드-워셜
▪
다익스트라 : 고정된 시작점에서 다른 모든 노드로 가는 최단거리를 구하는 알고리즘. 단, 음수 간선은 있으면 안됨
▪
벨만-포드 : 다익스트라와 똑같은데 음수 간선도 괜찮다는 점만 다름 (시간 여행, 웜홀 같은 상황)
▪
플로이드-워셜 : 시작점이 없고, 주어진 어떤 노드를 체크하더라도 두 타깃 간의 최단 거리를 구할 수 있음 (모든 도시 간의 최단 거리 구하기 같은 상황)(시간복잡도 좋지 않음)
◦
최소 신장 트리 : 최소 비용으로 간선을 써서 모든 노드 연결하는 알고리즘 (유니온 파인드가 내부적으로 필요함 → 사이클 나올 수 없게 방지해주는 데에 사용)
그래프의 표현
•
정의) 그래프 자료구조 구현
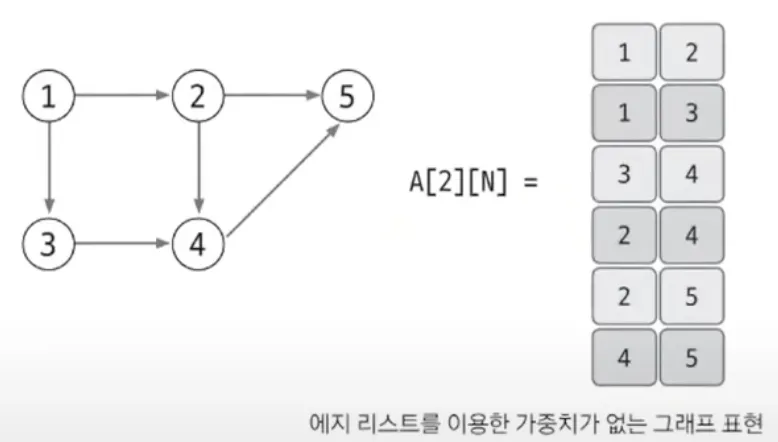
에지 리스트
•
정의) 에지를 중심으로 그래프 표현
•
표현)
◦
가중치 없는 그래프 표현
▪
첫 번째 행을 시작 노드, 두 번째 행을 종료 노드로 해서 이차원 배열로 표현
▪
방향이 없다면, 시작 노드와 종료 노드 뒤바꾼 두 쌍을 배열에 넣기
◦
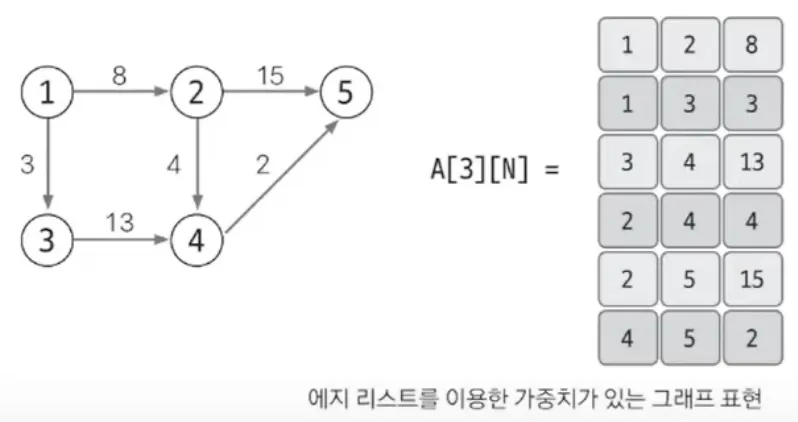
가중치 있는 그래프 표현
▪
첫 번째 행을 시작 노드, 두 번째 행을 종료 노드, 세 번째 행을 가중치로 해서 이차원 배열로 표현
•
특징)
◦
구현하기 쉬움
◦
에지를 중심으로 표현하다보니, 노드로 탐색하긴 어려움 (노드 중심 알고리즘에 잘 사용안함)
◦
벨만 포드, 크루스칼 알고리즘에 사용
인접 행렬
•
정의) 2차원 배열의 자료구조 이용해 그래프 표현
◦
노드 개수가 N개면, N*N 인접 행렬로 표현
◦
노드를 중심으로 그래프 표현
•
표현)
◦
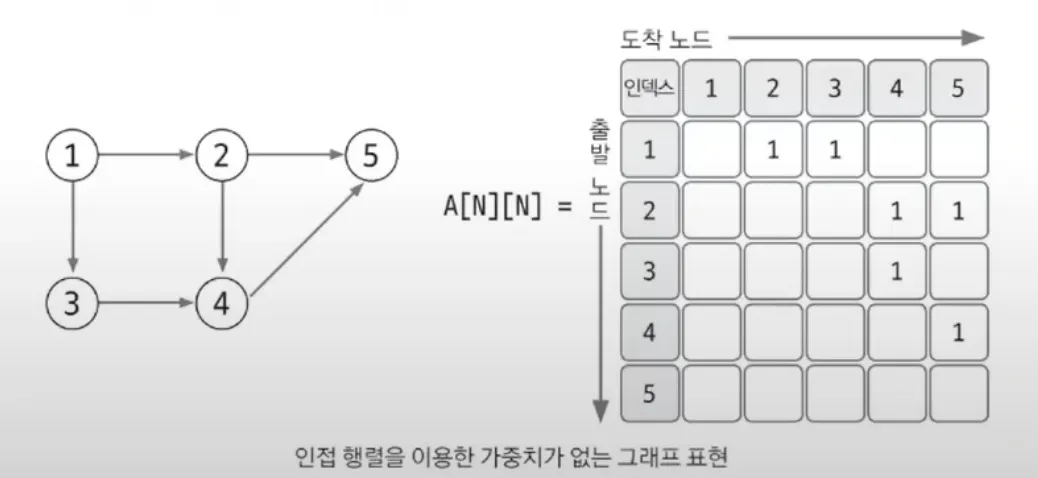
가중치 없는 그래프 표현
▪
인덱스를 이용해서 시작 노드와 도착 노드를 표현
▪
1에서 2로 향하는 에지를 1행 2열에 1(있다/없다)을 저장하는 방식으로 표현
◦
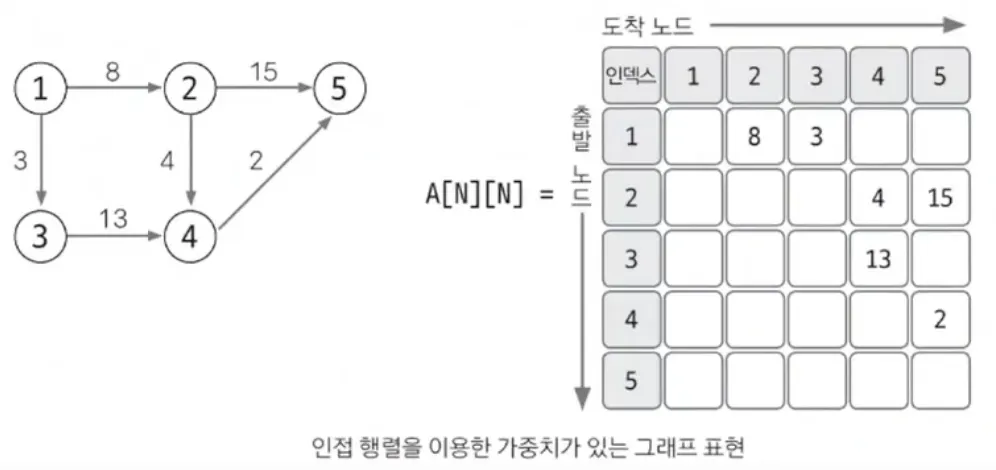
가중치 있는 그래프 표현
▪
1에서 2로 향하는 가중차 3의 에지를 1행 2열에 3(가중치)을 저장하는 방식으로 표현
•
특징)
◦
노드와 관련되어 있는 에지를 탐색하려면 N번 접근해야 해서 노드 개수에 비해 에지가 적을 때는 공간 효율성과 시간 효율성 떨어짐
▪
N개 전부 봐야 해서 오래 걸림 → ex. A[2][1]=0, A[2][2]=0, A[2][3]=0, A[2][4] = 4
▪
[N][N] 공간 필요함
◦
노드 개수에 따라 사용 여부 적절히 판단해야 함
▪
노드가 3만 개가 넘으면 자바 힙 스페이스 에러 발생
인접 리스트
•
정의) ArrayList로 그래프를 표현
◦
노드 개수만큼 ArrayList 선언
◦
노드를 중심으로 그래프 표현
•
표현)
◦
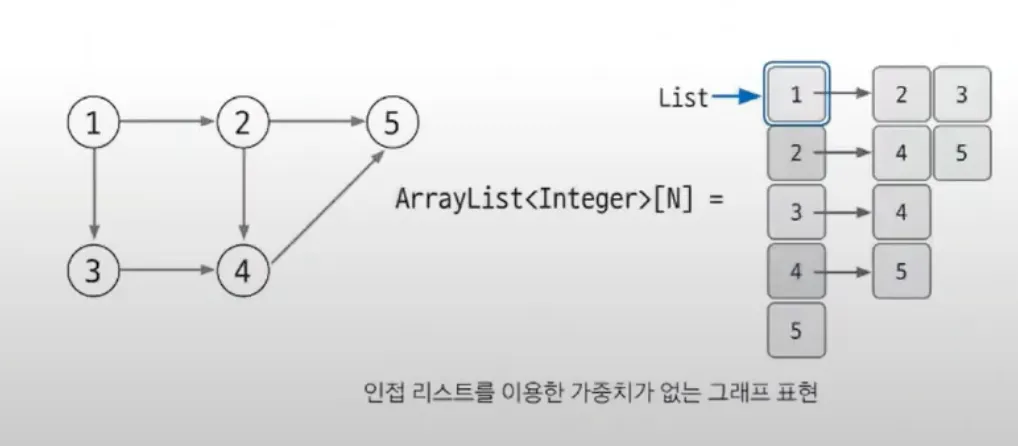
가중치 없는 그래프 표현
▪
N번 노드와 연결되어 있는 노드를 배열의 위치 N에 연결된 노드로 표현
▪
ArrayList의 배열 선언 → ArrayList<Integer>[N]
•
노드 추가 → A[3].add(4)
◦
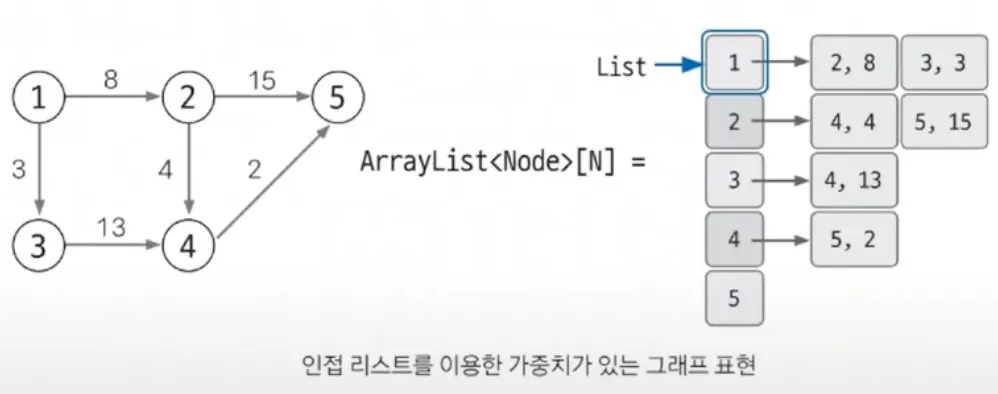
가중치 있는 그래프 표현 (매우 중요)
▪
(도착 노드, 가중치)를 갖는 Node 클래스를 선언해 ArrayList에 사용
▪
클래스 자료형을 사용하는 ArrayList의 배열 선언 → ArrayList<Node>[N]
•
노드 추가 → A[3].add(new Node(4, 3))
•
특징)
◦
가장 중요 → 인접 행렬로 풀릴 문제는 전부 인접 리스트로 풀리고, 실제로 그래프 알고리즘에선 에지 중심보단 노드 중심으로 도는 알고리즘이 더 많음
◦
구현 복잡한 편임
◦
노드와 연결되어 있는 에지를 탐색하는 시간 매우 뛰어남
◦
노드 개수가 커도 공간 효율이 좋아 메모리 초과도 발생하지 않음
참고