정의
•
하나의 시작 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘
특징
•
다익스트라: 한 지점에서 모든 지점까지  플로이드 워셜: 모든 지점에서 다른 모든 지점까지
플로이드 워셜: 모든 지점에서 다른 모든 지점까지
•
A*: 100% 정확한 최단거리 내지 않아도 되고, 정점의 개수가 많아 현실적으로 다익스트라 쓰기 어려운 경우 사용할 수 있는 근사 알고리즘
•
시간복잡도는 O(ElogE) (E: 에지 수)
◦
에지 한 개당 우선순위 큐에 최대 한 개의 원소가 추가될 수 있기 때문
◦
우선순위 큐에 N개의 원소를 추가하는 시간 복잡도 → O(NlogN)
•
우선순위 큐로 구현 가능
•
단계마다 방문하지 않은 노드 중 가장 최단 거리 짧은 노드 선택한 뒤에, 그 노드를 거쳐 가는 경우를 확인해 최단 거리를 갱신
◦
최단 거리 배열에서 현재 값이 가장 작은 노드 고르는 이유)
▪
현재 선택한 노드의 최단 거리가 앞으로 변경될 일 없는 고정된 결과여야 해서. 만일 고정된 결과가 아니라면, 다른 노드들에게 잘못된 최단 거리를 전파하게 됨.
◦
현재 최단 거리 배열에서 최단 거리가 가장 짧은 노드는 값이 더이상 변경될 일이 없다고 확신할 수 있는 이유)
▪
노드의 최단 거리는 다른 노드의 최단 거리 배열의 값(+ 에지 가중치)과 비교해 둘 중 작은 값으로 업데이트될 텐데, 현재 노드의 최단 거리 배열의 값이 배열에서 가장 작다면 다른 어떤 값과 비교해도 항상 더 작아서 업데이트될 일이 절대 없기 때문
◦
예시)
•
에지의 가중치가 모두 양수일 때만 사용 가능, 방향/무방향 여부는 상관 없이 사용 가능
◦
가중치가 음수인 에지가 있으면 사용할 수 없는 이유)
▪
현재 갈 수 있는 노드 중 가장 가까운 노드까지의 거리를 확정할 수 없기 때문
◦
예시)
추상화한 과정
1.
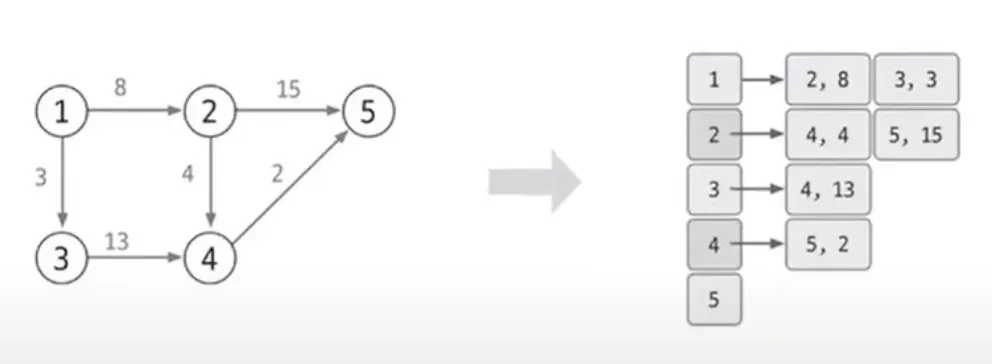
그래프를 인접 리스트로 구현하기
2.
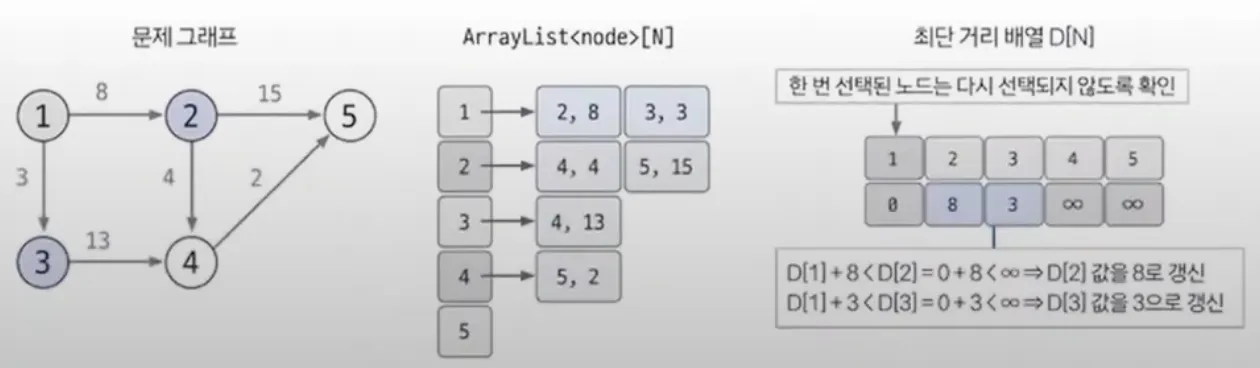
최단 거리 배열 초기화하기
•
출발 노드는 0, 이외의 노드는 무한(99_999_999 같이 적당히 큰 값)으로 초기화
3.
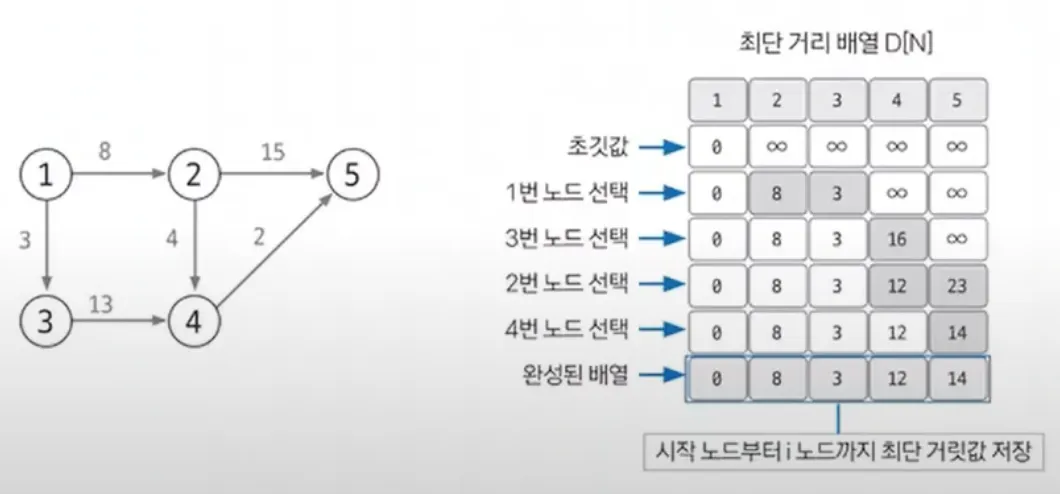
최단 거리 배열에서 현재 값이 가장 작은 노드 고르기
4.
최단 거리 배열 업데이트하기
•
현재 선택된 노드에 연결된 에지의 값을 바탕으로 현재 노드와 연결된 노드의 최단거리 값 업데이트
•
최단거리 값을 Min(선택 노드의 최단 거리 배열의 값 + 에지 가중치, 연결된 노드의 최단 거리 배열의 값) 으로 업데이트
5.
모든 노드가 처리될 때까지 과정 3~4를 반복해 최단 거리 배열 완성하기
•
과정 4에서 선택 노드가 될 때마다 다시 선택되지 않도록 방문 배열 만들어 처리
구체화한 과정
1.
우선순위 큐에 (거리,노드) 꼴로 (0, 시작점)을 추가, 최단 거리 배열에 시작점은 0으로, 나머지는 큰 수로 초기화
2.
우선순위 큐에서 거리가 가장 작은 원소(노드)를 선택 (pop)
•
해당 원소의 거리가 최단 거리 테이블에 있는 값과 다를 경우 3번 과정을 수행하지 않고 넘어감
◦
원소의 거리가 최단 거리 테이블에 있는 값과 다르다는 건 해당 원소가 우선순위 큐에 들어온 이후로 더 짧은 경로가 등장해서 현재는 쓸모가 없어진 원소라는 의미임
◦
우선순위 큐에 원소가 들어오는 상황은, 항상 거리가 더 줄어들었을 때 최단 거리 테이블을 갱신하며 우선순위 큐에 들어온 상황이기 때문임
◦
따라서 원소의 거리가 최단 거리 테이블에 있는 값과 다를 땐 해당 원소의 거리는 최단 거리 테이블에 있는 값보다 무조건 더 큼 → 의미 없는 값
3.
선택한 노드와 이웃한 노드들에 대해
•
현재 본인의 최단 거리 테이블 값(최단 거리)보다
•
선택한 노드를 거쳐가는 것이 더 작은 값을 가질 경우
•
최단 거리 테이블 값을 갱신하고 우선순위 큐에 (거리,노드)를 추가
4.
우선순위 큐가 빌 때까지 2~3번 과정을 반복
코드 1
0.
가중치 있는 그래프를 인접리스트로 표현하기
1.
우선순위 큐에 (거리, 노드)꼴로 (0, 시작점)을 추가, 최단 거리 배열에 시작점은 0으로, 나머지는 큰 수로 초기화
2.
우선순위 큐에서 거리가 가장 작은 원소를 pop하여 선택하고, 원소의 거리가 최단 거리 배열의 값과 같은지 확인
3.
선택한 노드와 이웃한 노드들의 최단 거리 갱신되어야 하면, 최단 거리 테이블 값 변경하고 우선순위 큐에 (거리, 노드)를 추가
•
최단 거리 계산 : min(선택 노드의 최단 거리+에지 가중치, 이웃 노드의 최단 거리)
•
최단 거리 갱신 조건 : "선택 노드의 최단 거리+에지 가중치"가 "이웃 노드의 최단 거리"보다 더 작을 때만 최단 거리 갱신
4.
우선순위 큐 빌 때까지 2,3을 반복
private static final int INFINITE = 99_999_999;
private static class Edge implements Comparable<Edge> {
int weight;
int node;
private Edge(int weight, int node) {
this.weight = weight;
this.node = node;
}
public int compareTo(Edge e) {
if (this.weight > e.weight) {
return 1;
} else {
return -1;
}
}
}
// numbers[edge+1][3]는 edge개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수(u, v, w)로 구성. 세 정수는 u에서 v로 가는 가중치 w인 간선을 의미
private static void solution(int vertex, int edge, int start, int[][] numbers) {
// 0. 가중치 있는 그래프를 인접리스트로 표현하기
ArrayList<Edge>[] graph = new ArrayList[vertex + 1];
for (int i = 1; i <= vertex; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 1; i <= edge; i++) {
int u = numbers[i][0];
int v = numbers[i][1];
int w = numbers[i][2];
graph[u].add(new Edge(w, v));
}
// 1. 우선순위 큐에 (거리, 노드)꼴로 (0, 시작점)을 추가, 최단 거리 배열에 시작점은 0으로, 나머지는 큰 수로 초기화
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(0, start));
int[] distance = new int[vertex + 1];
for (int i = 1; i <= vertex; i++) {
distance[i] = INFINITE;
if (i == start) {
distance[i] = 0;
}
}
while (!pq.isEmpty()) {
// 2. 우선순위 큐에서 거리가 가장 작은 원소를 pop하여 선택하고, 원소의 거리가 최단 거리 배열의 값과 같은지 확인
Edge select = pq.poll();
if (select.weight != distance[select.node]) {
continue;
}
// 3. 선택한 노드와 이웃한 노드들의 최단 거리 갱신되어야 하면, 최단 거리 테이블 값 변경하고 우선순위 큐에 (거리, 노드)를 추가
// 최단 거리 갱신 조건 : "선택 노드의 최단 거리+에지 가중치"가 "이웃 노드의 최단 거리"보다 더 작을 때만 최단 거리 갱신
for (Edge near : graph[select.node]) {
if (distance[select.node] + near.weight >= distance[near.node]) {
continue;
}
distance[near.node] = distance[select.node] + near.weight;
pq.add(new Edge(distance[near.node], near.node));
}
}
}
Java
복사
코드 2
위 코드가 잘 이해되신 분들을 위한 구현이 더 간단하지만 조금 덜 직관적인 코드
0.
가중치 있는 그래프를 인접리스트로 표현하기
1.
우선순위 큐에 (거리, 노드)꼴로 (0, 시작점)을 추가, 최단 거리 배열은 큰수로 초기화
2.
우선순위 큐에서 거리가 가장 작은 원소를 선택(pop)하고, 한 번도 선택된 적이 없는 노드라면 최단 거리 배열에 원소의 가중치 값 넣기
3.
선택한 노드와 이웃한 노드가 한 번도 선택된 적이 없는 노드라면, 우선순위 큐에 (거리, 노드)를 추가
4.
우선순위 큐 빌 때까지 2,3을 반복
달라진 점
•
최단 거리 배열을 굳이 매번 갱신하지 않고,
•
최단 거리임이 확정된 원소만 값을 저장
// 위는 동일
// 1. 우선순위 큐에 (거리, 노드)꼴로 (0, 시작점)을 추가, 최단 거리 배열은 큰수로 초기화
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(0, start));
int[] distance = new int[vertex + 1];
for (int i = 1; i <= vertex; i++) {
distance[i] = INFINITE; // start값도 infinite로 두기
}
while (!pq.isEmpty()) {
// 2. 우선순위 큐에서 거리가 가장 작은 원소를 선택(pop)하고, 한 번도 선택된 적이 없는 노드라면 최단 거리 배열에 원소의 가중치 값 넣기
Edge select = pq.poll();
if (distance[select.node] != INFINITE) {
continue;
}
distance[select.node] = select.weight;
// 3. 선택한 노드와 이웃한 노드가 한 번도 선택된 적이 없는 노드라면, 우선순위 큐에 (거리, 노드)를 추가
for (Edge near : graph[select.node]) {
if (distance[near.node] != INFINITE) {
continue;
}
pq.add(new Edge(distance[select.node] + near.weight, near.node));
}
}
Java
복사
참고