본 게시글은 하단 책을 읽고 학습한 내용을 제 생각으로 요약, 정리한 글입니다.
1. 퍼셉트론이란?
1) 퍼셉트론 알고리즘
•
정의) 다수의 신호를 입력으로 받아 하나의 신호를 출력
•
특징)
◦
신경망의 기원이 되는 알고리즘
◦
신호: 흐름이 있는 것
▪
1 → 신호가 흐름
▪
0 → 신호가 흐르지 않음
•
예시)
◦
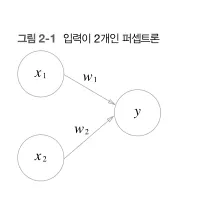
2개의 신호를 입력으로 받은 퍼셉트론
▪
그림)
▪
용어)
•
: 입력 신호
•
: 출력 신호
•
: 가중치 → 각 신호가 결과에 주는 영향력을 조절
◦
가중치가 클 수록 해당 신호가 중요하단 의미
•
원: 뉴런 == 노드
▪
동작 원리)
•
입력 신호는 보내질 때 각각 고유한 고중치가 곱해짐
•
도착한 신호의 총합이 임계값(정해진 한계, )을 넘어서면 1 출력
◦
신호가 흐른단 의미
2. 퍼셉트론 구현
1) 구현 방법
1.
진리표: 입력 신호와 출력 신호의 대응 표
2.
진리표대로 작동하도록 가중치와 임계값을 정함
3.
를 -b로 치환
•
b : 편향
4.
가중치와 편향 도입해 구현
2) AND 게이트
진리표
•
가중치와 임계값 이용해 구현
◦
가 모두 1일 때만 가중 신호 총합이 임계값 웃돌게 함
◦
가중치와 임계값
▪
(0.5, 0.5, 0.7) (0.5, 0.5, 0.8) (1.0, 1.0, 1.0)… → 무수히 많음
코드
•
가중치와 편향 도입해 구현
코드
3) NAND 게이트 (Not And)
진리표 : and 게이트 출력 뒤집은 것
•
가중치와 편향 도입해 구현
◦
가중치와 임계값
▪
(-0.5, -0.5, -0.7)… → AND 게이트 매개변수 부호 모두 반전한 것
코드
4) OR 게이트
진리표
•
가중치와 편향 도입해 구현
◦
가중치와 임계값
▪
(0.5, 0.5, 0.2)…
코드
•
구현 가능 (선형)
퍼셉트론 시각화
◦
linear한 decision boundary로 분류 가능 → 퍼셉트론으로 구현 가능
▪
직선으로 세모와 동그라미 분류 가능
예시) 가중치와 임계값: (1.0, 1.0, 0.5)
3. 퍼셉트론의 한계
1) xor 게이트 (배타적 논리합)
진리표
•
구현 불가능 (비선형)
퍼셉트론 시각화
◦
곡선으로 분류 가능 → 퍼셉트론으로 구현 불가능
2) 선형과 비선형, 퍼셉트론의 한계
•
퍼셉트론의 한계: 직선 하나로 나눈 영역만 표현 가능
◦
선형: 직선 영역 / 비선형: 곡선 영역
◦
해결) 층을 쌓아 다층 퍼셉트론을 만듦
4. 다층 퍼셉트론
1) 기존 게이트 조합해 XOR 게이트 만들기
조합 회로
진리표
2) XOR 게이트 구현
•
다층 퍼셉트론
◦
정의) 층이 여러 개인 퍼셉트론
그림) 단층 퍼셉트론 vs 다층 퍼셉트론(2층 퍼셉트론)
◦
과정)
▪
1) 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호 보냄
▪
2) 1층의 뉴런이 2층의 뉴런으로 신호 보내고, 2층의 뉴런은 y를 출력함
◦
특징) 단층 퍼셉트론으론 표현하지 못한 것을 층을 늘려 구현할 수 있음
◦
예시) XOR 게이트 구현
코드