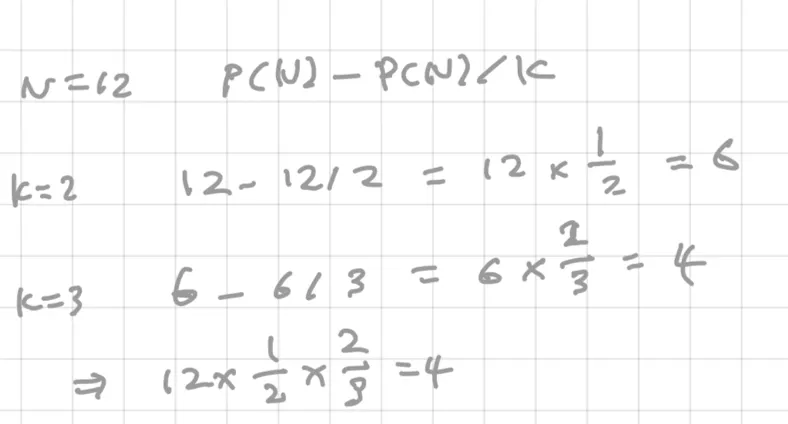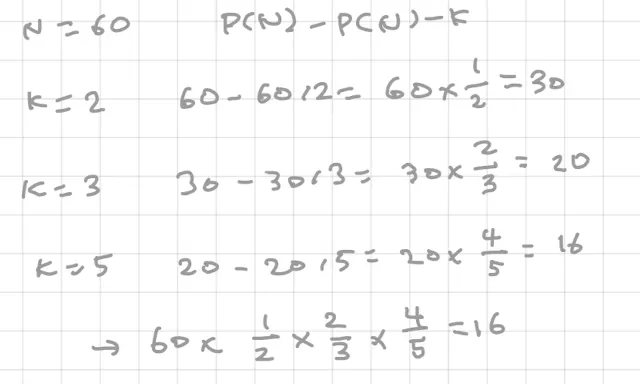1. 소수 구하기 (단순 판정)
•
정의) 어떤 수가 소수(1과 자기 자신 외에 약수가 존재하지 않는 수)인지 아닌지 확인하기
•
특징)
◦
어떤 수 N이 소수인지 판별하고 싶다면, N을 2부터 N-1까지의 수로 나누어서 나누어떨어지는 경우가 있는지 보면 단순하게 알 수 있음
▪
이때, N-1까지 해도 무방하지만 시간 복잡도를 줄이기 위해 까지만 봐도 무방함
증명
•
예를 들어 N이 12라면 N의 약수는 1,2,3,4,6,12 인데,
◦
2와 6은 짝꿍이고, 3과 4 역시 짝꿍이기 떄문임 (2*6=12, 3*4=12)
◦
2와 3만 알아도 4와 6은 자동으로 알 수 있음
•
다른 예로 N이 16이라면 N의 약수는 1,2,4,8,16인데,
◦
2와 8은 짝꿍이고, 4는 자기자신과 짝꿍임
◦
따라서 2와 4까지만 알면 됨
•
다른 예로 N이 25라면 N의 약수는 1, 5, 25인데,
◦
5로 나눠봐야지만 25가 소수인지 합성수인지 알 수 있음
◦
즉, 까지는 살펴봐야 된단 의미임
•
코드)
private static boolean isPrime(int n) {
if (n == 1) return 0;
for (int i = 2; i < n; i++) {
if (n % i == 0) return false;
}
return true;
}
Java
복사
◦
최적화 한 코드
private static boolean isPrime(int n) {
if (n == 1) return 0;
for (int i = 2; i * i <= n; i++) { // n의 제곱근까지만 검사하는 이유
if (n % i == 0) return false;
}
return true;
}
Java
복사
◦
for (int i = 2; i * i <= n; i++) { // n의 제곱근까지만 검사하는 이유
▪
n의 약수 중 1이 아닌 가장 작은 수를 구하면 끝나는 문제인데,
▪
1이 아닌 가장 작은 약수는 무조건 n의 제곱근()보다 작음
2. 소수 구하기 (에라토스테네스의 체)
•
정의) 어떤 범위 내에서 소수들을 구해야 할 때 효과적으로 소수를 구하기 위해 ‘에라토스테네스의 체’라는 판별법 사용할 수 있음
•
특징)
◦
시간복잡도 : O(Nlog(logN))
▪
이중 for문을 이용하므로 시간 복잡도가 O(N^2)처럼 보이지만,
▪
배수를 삭제하는 연산으로 실제 구현에선 바깥쪽 for문을 생략하는 경우가 빈번하게 발생하기 때문
•
과정)
1.
구하고자 하는 소수의 범위만큼 1차원 배열 생성
2.
2부터 시작해서 숫자를 하나씩 살펴보는데, 현재 선택된 숫자가 지워지지 않은 상태라면 현재 선택된 숫자의 배수에 해당하는 수들을 배열에서 끝까지 탐색하면서 지움. 이때 처음으로 선택한 숫자는 지우지 않음
3.
배열의 끝까지 2를 반복한 후 배열에서 남아있는 모든 수를 출력
•
코드)
boolean[] isPrime = new boolean[n + 1]; // 1~n까지. 소수인지 여부 (isPrime[3]=true면 3이 소수라는 뜻)
Arrays.fill(isPrime, true); // 전부 true로 초기화
isPrime[1] = false; // 1은 합성수니 false로 미리 지정
for (int i = 2; i <= n; i++) {
if (isPrime[i]) {
for (int j = i * 2; j <= n; j += i) {
isPrime[j] = false;
}
}
}
ArrayList<Integer> prime = new ArrayList<>();
for (int i = 2; i <= n; i++) {
if (isPrime[i]) prime.add(i);
}
int[] answer = prime.stream().mapToInt(i -> i).toArray();
Java
복사
◦
최적화한 코드)
// ...
for (int i = 2; i * i <= n; i++) { // n의 제곱근까지만 검사
if (isPrime[i]) {
for (int j = i * i; j <= n; j += i) { // i의 제곱부터 제외
isPrime[j] = false;
}
}
}
// ...
Java
복사
◦
for (int i = 2; i * i <= n; i++) // n의 제곱근까지만 검사하는 이유
▪
n이 16이라면, 1, 2, 4, 8, 16중 4까지만 봐도 되는데 그 이유는
▪
5*2, 5*3은 이미 앞에서 봤고(2,3검사할 때)
▪
5*5부터는 16 훌쩍 넘어가서 안봐도 되기 때문임
◦
for (int j = i * i; j <= n; j += i) // i의 제곱부터 제외
▪
i가 5라면, 5*2, 5*3, 5*4는 이미 false로 되어 있으므로, 5*5부터 보면됨
3. 오일러 피
•
정의) 오일러 피 함수 P[N]의 정의는 1부터 N까지 범위에서 N과 서로소(공약수가 1 이외에 없는 관계)인 자연수의 개수를 의미함
◦
ex) P[6] = 1~6 범위에서 6과 서로소인 자연수 개수 = 2 (1과 5)
•
과정)
1.
구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스값으로 초기화
2.
2부터 시작해서 현재 배열의 값과 인덱스가 같으면(소수일 때) 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열에 끝까지 탐색하며 P[i] = P[i] - P[i]/K 연산을 수행(i는 k의 배수)
3.
배열의 끝까지 2를 반복하며 오일러 피 함수를 완성
•
팁)
◦
그림 거꾸로 이해해보기
▪
N의 소인수(소수인 약수)들을 K로 두고 P(i)-P(i)/K 연산을 진행함
•
예를 들어 N=12는 K=2, K=3(12의 소인수 : 2, 3)일 때 P(i)-P(i)/K 연산을 진행했음을 위 그림에서 확인할 수 있음
▪
P(i)-P(i)/K 는 어떤 수 P(i)에 대해 K의 배수의 개수만큼 뺀 다 생각하면 좀 더 직관적으로 이해될 수 있음(사람에 따라서)
•
예시)
증명) 어떻게 갱신된 값을 사용해서 나눠도 나누어 떨어지는 게 보장될까?
•
즉, 맨 처음을 보면 K=2일 때 N이 2로 나누어떨어지는 값들에 대해 P(i)-P(i)/K 연산을 수행하면
◦
N-N/2를 하는 꼴이니 문제가 없어보이지만 (초기엔 P(N)==N 이었어서)
•
그 후에 K=3일 때를 보면 마찬가지로 N이 3으로 나누어떨어지는 값들에 대해 P(i)-P(i)/K 연산을 수행할 텐데,
◦
P(i)-P(i)/3을 하려 보니 이번엔 P(N)==N인게 보장되지 않음. P(N)이 아까 전에 K=2일 때 다른 값으로 갱신된 애들이 존재하기 때문임. 그렇다면 누군지 모르겠는 P(N) 값이 3으로 나누어떨어지는 걸 보장할 수 있을까?
◦
예를 들면 N=12인 경우가 그 예인데,
▪
K=2일 때 N=12가 K로 나누어 떨어지기에 P(i)-P(i)/k 연산을 수행하면 12-12/2=6으로 납득이 쉽지만
▪
K=3일 때 N=12가 K로 나누어 떨어지기에 P(i)-P(i)/k 연산을 수행하려 보니, P(i)가 위에서 갱신된 6이라서 6-6/3 를 계산해야 함
▪
이때, 6은 과연 3으로 나누어 떨어진단 걸 보장할 수 있을까?
▪
정답은 “보장할 수 있다”임
▪
우리는 12의 소인수(소수인 약수)들에 대해 P(i)-P(i)/k 연산을 수행하기 때문임
▪
K=2와 K=3 모두 12의 소인수들임
▪
애초에 소수인 수들의 배수에 대해 연산을 수행하는데, 이를 연산 당하는 입장에서 거꾸로 보면 소수인 약수들에 대해 연산이 수행되는 거임
▪
이때 우리는 소인수의 배수의 개수들만큼 뺄 거고, 식을 다시 정리해보면 아래와 같음
▪
결국 오일러 피 공식은 아래와 같이 정리할 수 있는데, 분모에 들어간 2와 3은 우리가 정의한 K로 12의 소인수이기에 무조건 약분됨. 즉 12를 나누어떨어지게 함.
▪
12를 2로 나누고 그 결과인 6을 다시 3으로 나누는 게 나누어떨어진단걸 보장할 수 있었던 이유임.
◦
추가적인 예로 N=60일 때를 봐보자.
▪
60의 소인수는 2,3,5 임.
▪
K=2일 때 60-60/2=30 으로 60의 서로소 후보 중 2의 배수들인 30개가 제외됨.
▪
K=3일 때 30-30/3=20 로 60의 서로소 후보 중 3의 배수들인 20개가 아닌 10개가 제외됨. 나머지 10개는 2의 배수에서 미리 제거됐음.
▪
K=5일 때 20-20/5=16로 60의 서로소 후보 중 5의 배수들인 12개가 아닌 4개가 제거됨. 나머지 8개는 2와 3의 배수에서 미리 제거됐음.
▪
그렇다면, 30이 3으로 나누어 떨어지는 것과 10이 5로 나누어 떨어지는 것은 어떻게 보장되는 걸까?
▪
정답은 배수의 개수와 연관됨. 처음에 2의 배수의 개수들만큼 제외했는데, 그 개수는 30으로 60/2를 의미함
▪
다음으로 30에서 3의 배수의 개수들만큼 뺐는데, 3의 배수의 개수는 10개로, 30/3을 의미함.
▪
이걸 식으로 정리해보면 아래와 같음
▪
결국 60을 2와 3과 5로 나눠야 하는 건데 당연히 가능함. 2와 3과 5는 60의 소인수였기 때문임.
참고